Тест соотношения - Ratio test

В математике , то тест соотношения является испытанием (или «критерий») для сходимости в виде ряда

${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} а_ {п},}$

где каждый член является реальным или комплексным числом и _п равно нулю , когда п велико. Тест был впервые опубликован Жаном ле Рондом Даламбером и иногда известен как критерий отношения Даламбера или критерий отношения Коши .

Тест

Диаграмма принятия решений для теста соотношения

В обычной форме теста используется предел

${\ displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |.}$

( 1 )

Тест соотношения утверждает, что:

• если L <1, то ряд абсолютно сходится ;
• если L > 1, то ряд расходится ;
• если L = 1 или предел не существует, то проверка неубедительна, поскольку существуют как сходящиеся, так и расходящиеся ряды, удовлетворяющие этому случаю.

Можно сделать тест отношения применимым к определенным случаям, когда предел L не существует, если используются верхний предел и нижний предел . Критерии тестирования также могут быть уточнены так, чтобы тест иногда был окончательным даже при L = 1. Более конкретно, пусть

${\ Displaystyle R = \ lim \ sup \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$

${\ displaystyle r = \ lim \ inf \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$.

Затем тест соотношения утверждает, что:

• если R <1, ряд абсолютно сходится;
• если r > 1, ряд расходится;
• если при всех больших n (независимо от значения r ) ряд также расходится; это потому , что отлично от нуля и растут , и , следовательно _п не стремится к нулю;${\ displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | \ geq 1}$${\ displaystyle | a_ {n} |}$
• в остальном тест не дает результатов.

Если предел L в ( 1 ) существует, должно быть L = R = r . Таким образом, исходный тест на соотношение является более слабой версией усовершенствованного.

Примеры

Сходится, потому что L <1

Рассмотрим серию

${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} {\ гидроразрыва {п} {е ^ {п}}}}$

Применяя критерий отношения, вычисляют предел

${\ displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ left | {\ frac {\ frac {n + 1} {e ^ {n + 1}}} {\ frac {n} {e ^ {n}}}} \ right | = {\ frac {1} { e}} <1.}$

Поскольку этот предел меньше 1, ряд сходится.

Дивергент, потому что L > 1

Рассмотрим серию

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {e ^ {n}} {n}}.}$

Помещая это в тест соотношения:

${\ displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ left | {\ frac {\ frac {e ^ {n + 1}} {n + 1}} {\ frac {e ^ {n}} {n}}} \ right | = e> 1.}$

Таким образом, серия расходится.

Безрезультатно, потому что L = 1

Рассмотрим три серии

${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} 1,}$

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {2}}},}$

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {n}}.}$

Первый ряд ( 1 + 1 + 1 + 1 + ) расходится, второй (центральный для задачи Базеля ) сходится абсолютно, а третий ( знакопеременный гармонический ряд ) сходится условно. Тем не менее, почтовые отношения величин трех рядов соответственно равны    и    . Итак, во всех трех случаях предел равен 1. Это показывает, что когда L = 1, ряды могут сходиться или расходиться, и, следовательно, исходный тест отношения неубедителен. В таких случаях требуются более точные тесты для определения сходимости или расхождения. ${\ displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$${\ displaystyle 1,}$   ${\ Displaystyle {\ гидроразрыва {п ^ {2}} {(п + 1) ^ {2}}}}$${\ displaystyle {\ frac {n} {n + 1}}}$${\ displaystyle \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$

Доказательство

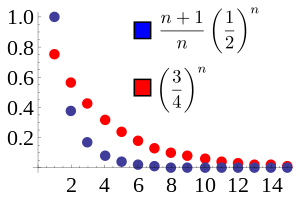
В этом примере отношение соседних членов в синей последовательности сходится к L = 1/2. Выбираем r  = (L + 1) / 2 = 3/4. Тогда в синей последовательности преобладает красная последовательность r ^k для всех n ≥ 2. Красная последовательность сходится, так что синяя последовательность также сходится.

Ниже приведено доказательство действительности первоначального теста соотношения.

Предположим, что . Затем мы можем показать, что ряд абсолютно сходится, показав, что его члены в конечном итоге станут меньше, чем члены определенного сходящегося геометрического ряда . Для этого рассмотрим действительное число r такое, что . Отсюда следует, что при достаточно большом n ; сказать, для всех п больше , чем N . Следовательно, для каждого n > N и i > 0, и поэтому ${\ displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | <1}$ ${\ Displaystyle L <г <1}$${\ displaystyle | a_ {n + 1} | <r | a_ {n} |}$${\ Displaystyle | а_ {п + я} | <г ^ {я} | а_ {п} |}$

${\ displaystyle \ sum _ {i = N + 1} ^ {\ infty} | a_ {i} | = \ sum _ {i = 1} ^ {\ infty} \ left | a_ {N + i} \ right | <\ sum _ {i = 1} ^ {\ infty} r ^ {i} | a_ {N} | = | a_ {N} | \ sum _ {i = 1} ^ {\ infty} r ^ {i} = | a_ {N} | {\ frac {r} {1-r}} <\ infty.}$

То есть ряд абсолютно сходится.

С другой стороны, если L > 1, то при достаточно большом n , так что предел слагаемых отличен от нуля. Следовательно, ряд расходится. ${\ displaystyle | a_ {n + 1} |> | a_ {n} |}$

Расширения для L = 1

Как видно из предыдущего примера, тест отношения может быть неубедительным, когда предел отношения равен 1. Однако расширения теста отношения иногда позволяют справиться с этим случаем.

Во всех приведенных ниже тестах предполагается, что Σ a _n является суммой с положительным a _n . Эти тесты также могут быть применены к любой серии с конечным числом отрицательных членов. Любая такая серия может быть записана как:

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n} = \ sum _ {n = 1} ^ {N} a_ {n} + \ sum _ {n = N + 1} ^ { \ infty} а_ {п}}$

где _N является самым проиндексирован термином отрицательного. Первое выражение справа - это частичная сумма, которая будет конечной, и поэтому сходимость всего ряда будет определяться свойствами сходимости второго выражения справа, которое может быть переиндексировано для формирования ряда всех положительные члены, начинающиеся с n = 1.

Каждый тест определяет тестовый параметр (ρ _n ), который определяет поведение этого параметра, необходимого для установления сходимости или расхождения. Для каждого теста существует более слабая форма теста, которая вместо этого накладывает ограничения на lim _{n-> ∞} ρ _n .

Все тесты имеют области, в которых они не могут описать свойства сходимости Σa _n . Фактически, никакой тест сходимости не может полностью описать свойства сходимости ряда. Это потому, что если Σa _n сходится, может быть найден второй сходящийся ряд Σb _n , который сходится медленнее: т. Е. Он обладает тем свойством, что lim _{n-> ∞} (b _n / a _n ) = ∞. Более того, если Σa _n расходится, может быть найден второй расходящийся ряд Σb _n , который расходится медленнее: т. Е. Он обладает тем свойством, что lim _{n-> ∞} (b _n / a _n ) = 0. В тестах сходимости по существу используется сравнение проверять на некотором конкретном семействе _n и терпеть неудачу для последовательностей, которые сходятся или расходятся медленнее.

Иерархия де Моргана

Огастес Де Морган предложил иерархию тестов отношения типа

Параметры теста отношения ( ) ниже все обычно включают термины формы . Этот член можно умножить на, чтобы получить доход . Этот термин может заменить прежний термин в определении параметров испытаний, и сделанные выводы останутся прежними. Соответственно, не будет никакого различия между ссылками, которые используют ту или иную форму параметра теста. ${\ displaystyle \ rho _ {n}}$${\ displaystyle D_ {n} a_ {n} / a_ {n + 1} -D_ {n + 1}}$${\ Displaystyle а_ {п + 1} / а_ {п}}$${\ displaystyle D_ {n} -D_ {n + 1} a_ {n + 1} / a_ {n}}$

1. Тест отношения Даламбера.

Первый тест в иерархии Де Моргана - это тест отношения, описанный выше.

2. Тест Раабе

Это расширение связано с Джозефом Людвигом Раабе . Определять:

${\ displaystyle \ rho _ {n} \ Equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$

(и некоторые дополнительные термины, см. Али, Блэкберн, Фельд, Дурис (нет), Дурис2)

В сериале будут:

• Converge , когда существует с> 1 такое , что для всех п> N .${\ displaystyle \ rho _ {n} \ geq c}$
• Расхождение , когда для всех п> N .${\ Displaystyle \ rho _ {п} \ leq 1}$
• В противном случае тест будет безрезультатным.

Для предельной версии серия будет:

• Сходимся, если (включая случай ρ = ∞)${\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$
• Отклонитесь, если .${\ Displaystyle \ lim _ {п \ к \ infty} \ rho _ {n} <1}$
• Если ρ = 1, проверка неубедительна.

Когда вышеуказанный предел не существует, можно использовать верхний и нижний пределы. В сериале будут:

• Сходятся, если ${\ Displaystyle \ liminf _ {п \ к \ infty} \ ро _ {п}> 1}$
• Расходиться, если ${\ Displaystyle \ limsup _ {п \ rightarrow \ infty} \ ро _ {п} <1}$
• В противном случае тест будет безрезультатным.

Доказательство теста Раабе

Определяя , нам не нужно предполагать, что предел существует; если , то расходится, а если сумма сходится. ${\ displaystyle \ rho _ {n} \ Equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$${\ Displaystyle \ limsup \ rho _ {п} <1}$${\ Displaystyle \ сумма а_ {п}}$${\ displaystyle \ liminf \ rho _ {n}> 1}$

Доказательство проводится по существу сравнением с . Предположим сначала, что . Конечно если то по крупному , так и сумма расходится; тогда предположим, что . Существует такое , что для всех , то есть так . Таким образом , что означает, что for ; поскольку это показывает, что расходится. ${\ Displaystyle \ сумма 1 / п ^ {R}}$${\ Displaystyle \ limsup \ rho _ {п} <1}$${\ displaystyle \ limsup \ rho _ {n} <0}$${\ Displaystyle а_ {п + 1} \ geq а_ {п}}$${\ displaystyle n}$${\ Displaystyle 0 \ Leq \ limsup \ rho _ {п} <1}$${\ Displaystyle R <1}$${\ Displaystyle \ rho _ {п} \ leq R}$${\ Displaystyle п \ geq N}$${\ displaystyle a_ {n} / a_ {n + 1} \ leq \ left (1 + {\ frac {R} {n}} \ right) \ leq e ^ {R / n}}$${\ displaystyle a_ {n + 1} \ geq a_ {n} e ^ {- R / n}}$${\ displaystyle a_ {n + 1} \ geq a_ {N} e ^ {- R (1 / N + \ dots + 1 / n)} \ geq ca_ {N} e ^ {- R \ log (n)} = ca_ {N} / n ^ {R}}$${\ Displaystyle п \ geq N}$${\ Displaystyle R <1}$${\ Displaystyle \ сумма а_ {п}}$

Доказательство второй половины полностью аналогично, с большинством неравенств просто обратным. Нам нужно предварительное неравенство для использования вместо простого, которое использовалось выше: Fix и . Обратите внимание на это . Итак ; следовательно . ${\ Displaystyle 1 + т <е ^ {т}}$${\ displaystyle R}$${\ displaystyle N}$${\ displaystyle \ log \ left (1 + {\ frac {R} {n}} \ right) = {\ frac {R} {n}} + O \ left ({\ frac {1} {n ^ {2 }}}\Правильно)}$${\ displaystyle \ log \ left (\ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ right) = R \ left ({\ frac {1} {N}} + \ dots + {\ frac {1} {n}} \ right) + O (1) = R \ log (n) + O (1)}$${\ displaystyle \ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ geq cn ^ {R}}$

Предположим теперь, что . Рассуждая, как в первом абзаце, используя неравенство, установленное в предыдущем абзаце, мы видим, что существует такое, что для ; так как это показывает, что сходится. ${\ displaystyle \ liminf \ rho _ {n}> 1}$${\ displaystyle R> 1}$${\ displaystyle a_ {n + 1} \ leq ca_ {N} n ^ {- R}}$${\ Displaystyle п \ geq N}$${\ displaystyle R> 1}$${\ Displaystyle \ сумма а_ {п}}$

3. Тест Бертрана.

Это расширение связано с Джозефом Бертраном и Огастесом Де Морганом .

Определение:

${\ Displaystyle \ rho _ {n} \ Equiv n \ ln n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ ln n}$

Тест Бертрана утверждает, что сериал:

• Converge , когда существует с> 1 таким образом, что для всех п> N .${\ displaystyle \ rho _ {n} \ geq c}$
• Расхождение , когда для всех п> N .${\ Displaystyle \ rho _ {п} \ leq 1}$
• В противном случае тест будет безрезультатным.

Для предельной версии серия будет:

• Сходимся, если (включая случай ρ = ∞)${\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$
• Отклонитесь, если .${\ Displaystyle \ lim _ {п \ к \ infty} \ rho _ {n} <1}$
• Если ρ = 1, проверка неубедительна.

Когда вышеуказанный предел не существует, можно использовать верхний и нижний пределы. В сериале будут:

• Сходятся, если ${\ displaystyle \ liminf \ rho _ {n}> 1}$
• Расходиться, если ${\ Displaystyle \ limsup \ rho _ {п} <1}$
• В противном случае тест будет безрезультатным.

4. Расширенный тест Бертрана.

Это расширение, вероятно, впервые появилось у Маргарет Мартин. Краткое доказательство, основанное на тесте Куммера и без технических предположений (таких как, например, существование пределов), приводится в.

Пусть целое число, и пусть Обозначим й итерации из натурального логарифма , то есть и для любого , . ${\ displaystyle K \ geq 1}$${\ Displaystyle \ ln _ {(К)} (х)}$${\ displaystyle K}$${\ Displaystyle \ пер _ {(1)} (х) = \ пер (х)}$${\ Displaystyle 2 \ Leq K \ Leq K}$${\ Displaystyle \ пер _ {(к)} (х) = \ пер _ {(к-1)} (\ пер (х))}$

Предположим, что отношение , когда оно велико, может быть представлено в виде ${\ Displaystyle а_ {п} / а_ {п + 1}}$${\ displaystyle n}$

${\ displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {1} {n}} + {\ frac {1} {n}} \ sum _ {я = 1} ^ {K-1} {\ frac {1} {\ prod _ {k = 1} ^ {i} \ ln _ {(k)} (n)}} + {\ frac {\ rho _ { n}} {n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n)}}, \ quad K \ geq 1.}$

(Предполагается, что пустая сумма равна 0. С тест сводится к тесту Бертрана.) ${\ displaystyle K = 1}$

Значение может быть явно представлено в виде ${\ displaystyle \ rho _ {n}}$

${\ displaystyle \ rho _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n) +1}}} - 1 \ right) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n) .}$

Расширенный тест Бертрана утверждает, что серия

• Сойдутся, когда существует такая, что для всех .${\ displaystyle c> 1}$${\ displaystyle \ rho _ {n} \ geq c}$${\ displaystyle n> N}$
• Отклониться, когда за все .${\ Displaystyle \ rho _ {п} \ leq 1}$${\ displaystyle n> N}$
• В противном случае тест будет безрезультатным.

Для предельной версии серия

• Сходимся, если (включая случай )${\ displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$${\ Displaystyle \ rho = \ infty}$
• Отклонитесь, если .${\ Displaystyle \ lim _ {п \ к \ infty} \ rho _ {n} <1}$
• Если , тест безрезультатный.${\ displaystyle \ rho = 1}$

Когда вышеуказанный предел не существует, можно использовать верхний и нижний пределы. Сериал

• Сходятся, если ${\ displaystyle \ liminf \ rho _ {n}> 1}$
• Расходиться, если ${\ Displaystyle \ limsup \ rho _ {п} <1}$
• В противном случае тест будет безрезультатным.

Для применения расширенного теста Бертрана см. Процесс рождения и смерти .

5. Тест Гаусса

Это расширение принадлежит Карлу Фридриху Гауссу .

Предполагая, что a _n > 0 и r> 1 , если может быть найдена ограниченная последовательность C _n такая, что для всех n :

${\ displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {\ rho} {n}} + {\ frac {C_ {n}} {n ^ {r }}}}$

тогда серия будет:

• Сходятся, если ${\ displaystyle \ rho> 1}$
• Расходиться, если ${\ displaystyle \ rho \ leq 1}$

6. Тест Куммера.

Это расширение связано с Эрнстом Куммером .

Пусть ζ _n - вспомогательная последовательность положительных констант. Определять

${\ Displaystyle \ rho _ {n} \ Equiv \ left (\ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ right) }$

Тест Куммера утверждает, что серия будет:

• Сходимся, если существует такой, что для всех n> N. (Обратите внимание, это не то же самое, что сказать )${\ displaystyle c> 0}$${\ displaystyle \ rho _ {n} \ geq c}$${\ displaystyle \ rho _ {n}> 0}$
• Расходятся, если для всех n> N и расходятся.${\ Displaystyle \ rho _ {п} \ leq 0}$${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} 1 / \ zeta _ {п}}$

Для предельной версии серия будет:

• Сходимся, если (включая случай ρ = ∞)${\ Displaystyle \ lim _ {п \ к \ infty} \ rho _ {n}> 0}$
• Расходятся, если и расходятся.${\ displaystyle \ lim _ {п \ к \ infty} \ rho _ {n} <0}$${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} 1 / \ zeta _ {п}}$
• В противном случае тест будет безрезультатным.

Когда вышеуказанный предел не существует, можно использовать верхний и нижний пределы. Сериал будет

• Сходятся, если ${\ Displaystyle \ liminf _ {п \ к \ infty} \ ро _ {п}> 0}$
• Расходятся, если и расходятся.${\ Displaystyle \ limsup _ {п \ к \ infty} \ ро _ {п} <0}$${\ Displaystyle \ сумма 1 / \ zeta _ {п}}$

Особые случаи

Все тесты в иерархии Де Моргана, кроме теста Гаусса, можно легко рассматривать как частные случаи теста Куммера:

• Для проверки отношения пусть ζ _n = 1. Потом:

${\ displaystyle \ rho _ {Kummer} = \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) = 1 / \ rho _ {Ratio} -1}$

• Для критерия Раабе пусть ζ _n = n. Потом:

${\ Displaystyle \ rho _ {Kummer} = \ left (n {\ frac {a_ {n}} {a_ {n + 1}}} - (n + 1) \ right) = \ rho _ {Raabe} -1 }$

• Для теста Бертрана пусть ζ _n = n ln (n). Потом:

${\ displaystyle \ rho _ {Kummer} = n \ ln (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}}} \ right) - (n + 1) \ ln (n +1)}$

Используя и аппроксимируя для больших n , что незначительно по сравнению с другими членами, можно записать: ${\ Displaystyle \ пер (п + 1) = \ пер (п) + \ пер (1 + 1 / п)}$ ${\ Displaystyle \ пер (1 + 1 / п) \ вправо 1 / п}$${\ displaystyle \ rho _ {Kummer}}$

${\ displaystyle \ rho _ {Kummer} = n \ ln (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ ln (n) -1 = \ rho _ {Бертран} -1}$

• Для расширенного теста Бертрана пусть Из разложения в ряд Тейлора для больших мы приходим к приближению${\ displaystyle \ zeta _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n).}$${\ displaystyle n}$

${\ displaystyle \ ln _ {(k)} (n + 1) = \ ln _ {(k)} (n) + {\ frac {1} {n \ prod _ {j = 1} ^ {k-1 } \ ln _ {(j)} (n)}} + O \ left ({\ frac {1} {n ^ {2}}} \ right),}$

где предполагается, что пустой продукт равен 1. Тогда

${\ displaystyle \ rho _ {Kummer} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) {\ frac {a_ {n}} {a_ {n + 1} }} - (n + 1) \ left [\ prod _ {k = 1} ^ {K} \ left (\ ln _ {(k)} (n) + {\ frac {1} {n \ prod _ { j = 1} ^ {k-1} \ ln _ {(j)} (n)}} \ right) \ right] + o (1) = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n) -1 + o (1).}$

Следовательно,

${\ displaystyle \ rho _ {Kummer} = \ rho _ {ExtendedBertrand} -1.}$

Обратите внимание, что для этих четырех тестов, чем выше они находятся в иерархии Де Моргана, тем медленнее расходится ряд. ${\ displaystyle 1 / \ zeta _ {n}}$

Доказательство теста Куммера

Если тогда зафиксируем положительное число . Существует такое натуральное число , что для каждого${\ displaystyle \ rho _ {n}> 0}$${\ displaystyle 0 <\ delta <\ rho _ {n}}$${\ displaystyle N}$${\ displaystyle n> N,}$

${\ displaystyle \ delta \ leq \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1}.}$

Поскольку для каждого${\ displaystyle a_ {n + 1}> 0}$${\ displaystyle n> N,}$

${\ displaystyle 0 \ leq \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}.}$

В частности, для всех это означает, что, начиная с индекса, последовательность монотонно убывает и положительна, что, в частности, означает, что она ограничена снизу на 0. Следовательно, предел ${\ displaystyle \ zeta _ {n + 1} a_ {n + 1} \ leq \ zeta _ {n} a_ {n}}$${\ Displaystyle п \ geq N}$${\ displaystyle N}$${\ displaystyle \ zeta _ {n} a_ {n}> 0}$

${\ displaystyle \ lim _ {n \ to \ infty} \ zeta _ {n} a_ {n} = L}$ существуют.

Это означает, что положительный ряд телескопирования

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} \ left (\ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1} \ right)}$ сходится,

и поскольку для всех ${\ displaystyle n> N,}$

${\ displaystyle \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}}$

при прямом сравнении положительных рядов ряд сходится. ${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} \ дельта а_ {п + 1}}$

С другой стороны, если , то существует такое N , при котором возрастает . В частности, существует, для которого для всех , и поэтому расходится по сравнению с . ${\ displaystyle \ rho <0}$${\ displaystyle \ zeta _ {n} a_ {n}}$${\ displaystyle n> N}$${\ displaystyle \ epsilon> 0}$${\ displaystyle \ zeta _ {n} a_ {n}> \ epsilon}$${\ displaystyle n> N}$${\ displaystyle \ sum _ {n} a_ {n} = \ sum _ {n} {\ frac {a_ {n} \ zeta _ {n}} {\ zeta _ {n}}}}$${\ displaystyle \ sum _ {n} {\ frac {\ epsilon} {\ zeta _ {n}}}}$

Модификация Тонга теста Куммера

Тонг создал новую версию теста Куммера. См. Также дальнейшие обсуждения и новые доказательства. Приведенная модификация теоремы Куммера характеризует все положительные ряды, а сходимость или расходимость можно сформулировать в виде двух необходимых и достаточных условий: одного для сходимости, а другого - для расходимости.

• Серия сходится тогда и только тогда , когда существует положительная последовательность , такая , что${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} а_ {п}}$${\ displaystyle \ zeta _ {n}}$${\ Displaystyle п = 1,2, \ точки}$${\ displaystyle \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ geq c> 0.}$

• Серия расходится , если и только если существует положительная последовательность , такая , что и${\ Displaystyle \ сумма _ {п = 1} ^ {\ infty} а_ {п}}$${\ displaystyle \ zeta _ {n}}$${\ Displaystyle п = 1,2, \ точки}$${\ displaystyle \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ leq 0,}$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {\ zeta _ {n}}} = \ infty.}$

Тест второго отношения Али

Более точный тест соотношения - это второй тест соотношения: Для определения: ${\ displaystyle a_ {n}> 0}$

${\ Displaystyle L_ {0} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$

${\ Displaystyle L_ {1} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$

${\ Displaystyle L \ эквив \ макс (L_ {0}, L_ {1})}$

По второму тесту на соотношение серия будет:

• Сходятся, если ${\ displaystyle L <{\ frac {1} {2}}}$
• Расходиться, если ${\ displaystyle L> {\ frac {1} {2}}}$
• Если тогда тест не дает результатов.${\ displaystyle L = {\ frac {1} {2}}}$

Если вышеуказанные пределы не существуют, возможно, можно будет использовать верхние и нижние пределы. Определять:

${\ Displaystyle L_ {0} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$		${\ Displaystyle L_ {1} \ Equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$
${\ displaystyle \ ell _ {0} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$		${\ displaystyle \ ell _ {1} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$
${\ Displaystyle L \ эквив \ макс (L_ {0}, L_ {1})}$		${\ Displaystyle \ Ell \ Equiv \ мин (\ ell _ {0}, \ ell _ {1})}$

Тогда в сериале будут:

• Сходятся, если ${\ displaystyle L <{\ frac {1} {2}}}$
• Расходиться, если ${\ displaystyle \ ell> {\ frac {1} {2}}}$
• Если тогда тест не дает результатов.${\ displaystyle \ ell \ leq {\ frac {1} {2}} \ leq L}$

Тест отношения али${\ displaystyle m}$

Этот тест является прямым продолжением теста второго отношения. Ибо положительно определяют: ${\ Displaystyle 0 \ Leq К \ Leq м-1,}$${\ displaystyle a_ {n}}$

${\ Displaystyle L_ {k} \ Equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$

${\ Displaystyle L \ эквив \ макс (L_ {0}, L_ {1}, \ ldots, L_ {м-1})}$

По результатам теста отношения th серия будет: ${\ displaystyle m}$

• Сходятся, если ${\ displaystyle L <{\ frac {1} {m}}}$
• Расходиться, если ${\ displaystyle L> {\ frac {1} {m}}}$
• Если тогда тест не дает результатов.${\ displaystyle L = {\ frac {1} {m}}}$

Если вышеуказанные пределы не существуют, возможно, можно будет использовать верхние и нижние пределы. Для определения: ${\ Displaystyle 0 \ Leq К \ Leq м-1}$

${\ Displaystyle L_ {k} \ Equiv \ limsup _ {п \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ displaystyle \ ell _ {k} \ Equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ Displaystyle L \ эквив \ макс (L_ {0}, L_ {1}, \ ldots, L_ {м-1})}$		${\ Displaystyle \ Ell \ Equiv \ min (\ ell _ {0}, \ ell _ {1}, \ ldots, \ ell _ {m-1})}$

Тогда в сериале будут:

• Сходятся, если ${\ displaystyle L <{\ frac {1} {m}}}$
• Расходиться, если ${\ displaystyle \ ell> {\ frac {1} {m}}}$
• Если , то тест безрезультатный.${\ displaystyle \ ell \ leq {\ frac {1} {m}} \ leq L}$

Тест отношения Али-Дойче Коэна${\ displaystyle \ varphi}$

Этот тест является расширением теста th отношения. ${\ displaystyle m}$

Предположим, что последовательность является положительной убывающей последовательностью. ${\ displaystyle a_ {n}}$

Позвольте быть таким, что существует. Обозначим и предположим . ${\ Displaystyle \ varphi: \ mathbb {Z} ^ {+} \ to \ mathbb {Z} ^ {+}}$${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$${\ displaystyle \ alpha = \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$${\ Displaystyle 0 <\ альфа <1}$

Предположим также, что ${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {a _ {\ varphi (n)}} {a_ {n}}} = L.}$

Тогда в сериале будут:

• Сходятся, если ${\ Displaystyle L <\ альфа}$
• Расходиться, если ${\ displaystyle \ ell> \ alpha}$
• Если , то тест безрезультатный.${\ Displaystyle L = \ альфа}$

Смотрите также

• Корневой тест
• Радиус схождения

Сноски

использованная литература

• Д'Аламбер, J. (1768), Opuscules , V , стр. 171–183..
• Апостол, Том М. (1974), Математический анализ (2-е изд.), Addison-Wesley , ISBN 978-0-201-00288-1: §8.14.
• Кнопп, Конрад (1956), Бесконечные последовательности и серии , Нью-Йорк: Dover Publications, Bibcode : 1956iss..book ..... K , ISBN 978-0-486-60153-3: §3.3, 5.4.
• Рудин, Уолтер (1976), Принципы математического анализа (3-е изд.), Нью-Йорк: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
• «Критерий Бертрана» , Математическая энциклопедия , EMS Press , 2001 [1994]
• «Критерий Гаусса» , Энциклопедия математики , EMS Press , 2001 [1994]
• «Критерий Куммера» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Уотсон, Г. Н.; Whittaker, ET (1963), Курс современного анализа (4-е изд.), Cambridge University Press, ISBN 978-0-521-58807-2: §2.36, 2.37.