Построение Гольдберга – Кокстера - Goldberg–Coxeter construction

Многогранник Гольдберга (3,1) и геодезический многогранник (3,1). Многогранники Гольдберга и геодезические многогранники были предшественниками операции Гольдберга – Кокстера.

Конструкция Голдберга – Кокстера или операция Голдберга – Кокстера ( построение GC или операция GC ) - это графическая операция, определенная на правильных многогранных графах со степенью 3 или 4. Она также применима к двойственному графу этих графов, то есть графам с треугольником или четырехугольником " лица ". Конструкцию GC можно рассматривать как подразделение граней многогранника решеткой из треугольных, квадратных или гексагональных многоугольников, возможно, с перекосом относительно исходной грани: это расширение понятий, введенных многогранниками Гольдберга и геодезическими многогранниками . Конструкция GC в основном изучается в органической химии для ее применения к фуллеренам , но она применялась к наночастицам , автоматизированному проектированию , плетению корзин и общему изучению теории графов и многогранников .

Конструкция Голдберга – Кокстера может быть обозначена как , где - оперируемый граф, а - целые числа , и . ${\ Displaystyle GC_ {к, \ ell} (G_ {0})}$${\ displaystyle G_ {0}}$${\ displaystyle k}$${\ displaystyle l}$${\ displaystyle k> 0}$${\ displaystyle \ ell \ geq 0}$

История

Майкл Голдберг представил многогранник Голдберга в 1937 году. Бакминстер Фуллер ввел термин « геодезический купол » в 1940-х годах, хотя в значительной степени он держал математику, лежащую в основе куполов, в коммерческой тайне. Геодезические купола - это геометрический двойник (части) многогранника Гольдберга: полный геодезический купол можно рассматривать как геодезический многогранник , двойственный многограннику Гольдберга. В 1962 году Дональд Каспар и Аарон Клаг опубликовали статью о геометрии вирусных капсидов, в которой применялись и расширялись концепции Голдберга и Фуллера. HSM Coxeter опубликовал в 1971 году статью, содержащую большую часть той же информации. Каспар и Клуг были первыми, кто опубликовал наиболее общую правильную конструкцию геодезического многогранника, сделав название «конструкция Гольдберга – Кокстера» примером закона эпонимии Стиглера .

Открытие бакминстерфуллерена в 1985 году послужило стимулом для исследования других молекул со структурой многогранника Гольдберга. Термины «фуллерен Гольдберга – Кокстера» и «конструкция Гольдберга – Кокстера» были введены Мишелем Дезой в 2000 году. Это также первый случай, когда рассматривается случай степени 4.

Строительство

Этот раздел во многом следует за двумя статьями Deza et al.

Мастер полигонов

Решетки

n-регулярный	3	4
Домен	Эйзенштейн ${\ displaystyle a + bu}$	Гауссовский ${\ displaystyle a + bi}$
Смежный блок	${\ displaystyle {\ begin {align} u & = {\ frac {1} {2}} \ left (1 + i {\ sqrt {3}} \ right) \\ & = e ^ {{\ frac {1} {3}} \ pi i} = \ omega +1 \ конец {выровнено}}}$	${\ displaystyle i = {\ sqrt {-1}}}$
Норма ${\ Displaystyle т (а, б)}$	${\ displaystyle a ^ {2} + ab + b ^ {2}}$	${\ displaystyle a ^ {2} + b ^ {2}}$.
Главный многоугольник	${\ displaystyle (0, x, xu)}$	${\ displaystyle (0, x, x (1 + i), xi)}$

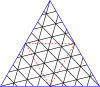
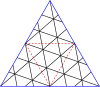
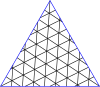
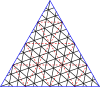
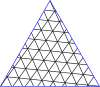
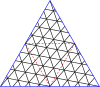
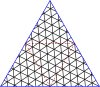
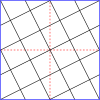
Регулярные решетки над комплексной плоскостью можно использовать для создания «мастер-многоугольников». В терминологии геодезических куполов это «структура разрыва» или «главный многогранный треугольник» (PPT). В 4-регулярном случае используется квадратная решетка над целыми гауссовскими числами , а в 3-регулярном случае используется треугольная решетка над целыми числами Эйзенштейна . Для удобства используется альтернативная параметризация целых чисел Эйзенштейна, основанная на корне шестой степени из единицы вместо третьего. В обычном определении целых чисел Эйзенштейна используется элемент . Норма определяется как квадрат абсолютного значения комплексного числа. Для 3-регулярных графов эта норма - это T-число или число триангуляции, используемое в вирусологии. ${\ textstyle \ omega = {\ frac {1} {2}} \ left (-1 + i {\ sqrt {3}} \ right) = e ^ {{\ frac {2} {3}} \ pi i } = u-1}$${\ Displaystyle т (к, \ ell)}$

Главный многоугольник - это равносторонний треугольник или квадрат, наложенный на решетку. В таблице справа приведены формулы для вершин главных многоугольников в комплексной плоскости, а в галерее ниже показаны главный треугольник и квадрат (3,2). Так что многоугольник можно описать одним комплексным числом, одна вершина устанавливается в 0. Есть несколько номеров , которые могут описать тот же многоугольник: это связывает друг с другом: если и ассоциированы, то в Eisensteins или в Гауссианы для некоторого целого числа . Набор элементов, которые являются ассоциированными друг с другом, является классом эквивалентности и элементом каждого класса эквивалентности, который имеет и является нормальной формой . ${\ displaystyle x}$${\ displaystyle y}$${\ Displaystyle х = и ^ {п} у}$${\ Displaystyle х = я ^ {п} у}$${\ displaystyle n}$${\ displaystyle a> 0}$${\ displaystyle b \ geq 0}$

• 

  (3,2) главный треугольник над треугольной сеткой

• 

  (3,2) мастер-квадрат над квадратной сеткой

Основные многоугольники и оператор можно классифицировать следующим образом: ${\ Displaystyle GC_ {к, \ ell} \ влево (G_ {0} \ right)}$

• Класс I: ${\ displaystyle \ ell = 0.}$
• Класс II: ${\ displaystyle k = \ ell.}$
• Класс III: все остальные. Операторы класса III существуют в киральных парах: является киральной парой .${\ Displaystyle GC_ {к, \ ell} \ влево (G_ {0} \ right)}$${\ displaystyle GC _ {\ ell, k} (G_ {0})}$

Ниже представлены таблицы главных треугольников и квадратов. Класс I соответствует первому столбцу, а класс II соответствует диагонали с немного более темным фоном.

Мастер полигонов для треугольников

Соедините треугольники через (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Мастер полигонов для квадратов

Мастер-квадраты через (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Композиция операций Гольдберга – Кокстера соответствует умножению комплексных чисел. Если и только если (т. Е. Последовательность операций слева дает граф, изоморфный графу справа), то для 3-регулярного графа принадлежит класс эквивалентности , а для 4-регулярного графа - эквивалентность класс . У этого есть несколько полезных последствий: ${\ displaystyle GC_ {a, b} \ left (GC_ {c, d} \ left (G_ {0} \ right) \ right) = GC_ {e, f} \ left (G_ {0} \ right)}$${\ Displaystyle (а + бу) (с + ду)}$${\ Displaystyle (е + фу)}$${\ Displaystyle (а + би) (с + ди)}$${\ Displaystyle (е + фи)}$

• Применение повторных операций Гольдберга – Кокстера коммутативно и ассоциативно .
• Комплексное сопряжение элемента или соответствует отражению построенного графа.${\ displaystyle a + bi}$${\ displaystyle a + bu}$
• Поскольку целые гауссовы и целые евклидовы числа являются евклидовой областью , элементы этих областей могут быть однозначно разложены на простые элементы. Следовательно, имеет смысл также разложить оператор Голдберга – Кокстера на последовательность «простых» операторов Голдберга – Кокстера, и эта последовательность является единственной (с точностью до перестановки).

Выполнение построения ГХ

Шаги построения GC следующие: ${\ Displaystyle GC_ {к, \ ell} (G_ {0})}$

1. Определить главный полигон, на основе , и${\ displaystyle k}$${\ displaystyle \ ell}$${\ displaystyle G_ {0}}$
2. Если вы работаете с 3- или 4-регулярным графом (вместо графа с треугольными / четырехугольными гранями), возьмите его двойственный граф . Этот двойственный граф будет иметь треугольные или четырехугольные грани.
3. Замените грани триангулированного / четырехугольного графа на главный многоугольник. Имейте в виду, что у плоских графов есть «внешняя» грань, которую также необходимо заменить. В приведенном ниже примере это делается путем прикрепления его к одной стороне графика и соединения других сторон по мере необходимости. Это временно вводит перекрывающиеся ребра в граф, но результирующий граф является плоским. Вершины можно переставить так, чтобы не было перекрывающихся ребер.
4. Если исходный граф был 3- или 4-регулярным графом, возьмите двойственный результат шага 3. В противном случае результатом шага 3 будет построение сборщика мусора.

Ниже приведен пример, где построен на каркасе из в кубе . На последних двух графиках синие линии являются краями , а черные линии - краями . (Пунктирные линии - это нормальные ребра графа, просто нарисованные по-разному, чтобы сделать перекрывающиеся ребра графа более видимыми.) Красные вершины находятся внутри и остаются внутри , в то время как синие вершины создаются заново при построении и находятся только внутри . ${\ displaystyle GC_ {1,1} (G_ {0})}$${\ displaystyle G_ {0}}$${\ displaystyle GC_ {1,1} (G_ {0})}$${\ displaystyle G_ {0}}$${\ displaystyle GC_ {1,1} (G_ {0})}$${\ displaystyle GC_ {1,1} (G_ {0})}$

• 

  Мастер-квадрат (1,1)

• 

  Стартовый многогранник (Куб)

• 

  ${\ displaystyle G_ {0}}$, скелет куба

• 

  Промежуточный этап строительства . ${\ displaystyle GC_ {1,1} (G_ {0})}$

• 

  Результат после перестановки ${\ displaystyle GC_ {1,1} (G_ {0})}$

• 

  Вложение результата ( ромбический додекаэдр )

Расширения

Конструкция Голдберга – Кокстера может быть легко расширена на некоторые неплоские графы, такие как тороидальные графы . Операторы класса III из-за их киральности требуют графа, который может быть вложен в ориентируемую поверхность , но операторы класса I и II могут использоваться на неориентируемых графах.

Смотрите также

Сноски

использованная литература