Неопределенная форма - Indeterminate form

В исчислении и других разделах математического анализа пределы, включающие алгебраическую комбинацию функций в независимой переменной, часто можно оценить, заменив эти функции их пределами ; если выражение, полученное после этой замены, не предоставляет достаточной информации для определения исходного предела, то выражение называется неопределенной формой . Более конкретно, неопределенна форма представляет собой математическое выражение , включающее не более двух , или , полученный путем применения теоремы алгебраическую предела в процессе попытки определить предел, который не в состоянии ограничить это значение предела один конкретный или бесконечность, и , таким образом , не определяет искомый предел. Предел, подтвержденный как бесконечность, не является неопределенным, поскольку было определено, что он имеет определенное значение (бесконечность). Термин был впервые введен учеником Коши Мойньо в середине 19 века. ${\ displaystyle 0 ~}$${\ displaystyle 1}$${\ displaystyle \ infty}$

В литературе обычно рассматриваются семь неопределенных форм:

${\ displaystyle {\ frac {0} {0}}, ~ {\ frac {\ infty} {\ infty}}, ~ 0 \ times \ infty, ~ \ infty - \ infty, ~ 0 ^ {0}, ~ 1 ^ {\ infty}, {\ text {and}} \ infty ^ {0}.}$

Наиболее распространенный пример неопределенной формы возникает при определении предела отношения двух функций, в котором обе эти функции стремятся к нулю в пределе, и упоминается как «неопределенная форма ». Например, в качестве подходов , отношений , и перейти к , и соответственно. В каждом случае, если подставить пределы числителя и знаменателя, результатом будет выражение , которое не определено. Грубо говоря, может принимать значения , или , и легко построить аналогичные примеры, для которых пределом является любое конкретное значение. ${\ displaystyle 0/0}$${\ displaystyle x}$${\ displaystyle 0 ~}$${\ Displaystyle х / х ^ {3}}$${\ Displaystyle х / х}$${\ Displaystyle х ^ {2} / х}$${\ displaystyle \ infty}$${\ displaystyle 1}$${\ displaystyle 0 ~}$${\ displaystyle 0/0}$${\ displaystyle 0/0}$${\ displaystyle 0 ~}$${\ displaystyle 1}$${\ displaystyle \ infty}$

Таким образом, учитывая , что две функции и как приближается , как приближается к некоторому предельной точки , в одиночку этот факт не дает достаточной информации для оценки предела${\ displaystyle f (x)}$${\ displaystyle g (x)}$${\ displaystyle 0 ~}$${\ displaystyle x}$ ${\ displaystyle c}$

Не всякое неопределенное алгебраическое выражение соответствует неопределенной форме. Например, выражение не определено как действительное число, но не соответствует неопределенной форме; любой определенный предел, порождающий эту форму, будет расходиться до бесконечности. ${\ displaystyle 1/0}$

Выражение, которое возникает другими способами, кроме применения алгебраической предельной теоремы, может иметь ту же неопределенную форму. Однако неуместно называть выражение «неопределенной формой», если выражение сделано вне контекста определения пределов. Так , например, которое возникает при подстановке для в уравнении не является формой неопределенными , поскольку это выражение не сделано при определении предела (это на самом деле не определено , как деление на ноль ). Другой пример - выражение . Оставлено ли это выражение неопределенным или равнозначным , зависит от области применения и может отличаться у разных авторов. Подробнее читайте в статье Ноль в степени нуля . Обратите внимание, что и другие выражения, содержащие бесконечность , не являются неопределенными формами . ${\ displaystyle 0/0}$${\ displaystyle 0 ~}$${\ displaystyle x}$${\ Displaystyle е (х) = | х | / (| х-1 | -1)}$${\ displaystyle 0 ^ {0}}$${\ displaystyle 1}$${\ displaystyle 0 ^ {\ infty}}$

Некоторые примеры и не примеры

Неопределенная форма 0/0

• 

  Рис.1: y =Икс/Икс

• 

  Рис.2: y =х ²/Икс

• 

  Рис.3: y =грех  х/Икс

• 

  Рис.4: y =х - 49/√ х - 7(для x = 49)

• 

  Рис.5: y =а х/Иксгде a = 2

• 

  Рис.6: y =Икс/х ³

Неопределенная форма особенно распространена в исчислении , потому что она часто возникает при оценке производных с использованием их определения в терминах предела. ${\ displaystyle 0/0}$

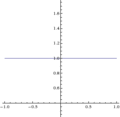
Как уже упоминалось выше,

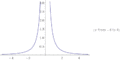
в то время как

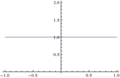
Этого достаточно, чтобы показать, что это неопределенная форма. Другие примеры с этой неопределенной формой включают ${\ displaystyle 0/0}$

а также

Прямая подстановка приближающегося числа в любое из этих выражений показывает, что эти примеры соответствуют неопределенной форме , но эти пределы могут принимать множество различных значений. Любое желаемое значение для этой неопределенной формы может быть получено следующим образом: ${\ displaystyle x}$${\ displaystyle 0/0}$${\ displaystyle a}$

Значение также может быть получено (в смысле расходимости до бесконечности): ${\ displaystyle \ infty}$

Неопределенная форма 0 ⁰

• 

  Рис.7: y = x ⁰

• 

  Рис.8: y = 0 ^x

Следующие ограничения показывают, что выражение является неопределенной формой: ${\ displaystyle 0 ^ {0}}$

Таким образом, в общем, зная, что и этого недостаточно, чтобы оценить предел ${\ displaystyle \ textstyle \ lim _ {x \ to c} f (x) \; = \; 0 \!}$${\ displaystyle \ textstyle \ lim _ {x \ to c} g (x) \; = \; 0}$

Если функции и являются аналитическими в и положительно при достаточно близкие (но не равны) , то предел будет . В противном случае используйте преобразование в таблице ниже, чтобы оценить предел. ${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle c}$${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle c}$${\ Displaystyle е (х) ^ {г (х)}}$${\ displaystyle 1}$

Выражения, не являющиеся неопределенными формами

Выражение обычно не рассматривается как неопределенная форма, потому что, если предел существует, тогда нет двусмысленности в отношении его значения, поскольку оно всегда расходится. Конкретно, если подходит и подходит , то и может быть выбрано так, чтобы: ${\ displaystyle 1/0}$${\ displaystyle f / g}$${\ displaystyle f}$${\ displaystyle 1}$${\ displaystyle g}$${\ displaystyle 0 ~}$${\ displaystyle f}$${\ displaystyle g}$

1. ${\ displaystyle f / g}$ подходы ${\ displaystyle + \ infty}$
2. ${\ displaystyle f / g}$ подходы ${\ displaystyle - \ infty}$
3. Лимита не существует.

В каждом случае абсолютное значение приближается , и поэтому частное должно расходиться в смысле расширенных действительных чисел (в рамках проективно расширенной вещественной линии пределом является бесконечность без знака во всех трех случаях). Точно так же любое выражение формы с (включая и ) не является неопределенной формой, так как частное, порождающее такое выражение, всегда будет расходиться. ${\ displaystyle | f / g |}$${\ displaystyle + \ infty}$${\ displaystyle f / g}$ ${\ displaystyle \ infty}$${\ displaystyle a / 0}$${\ Displaystyle а \ neq 0}$${\ Displaystyle а = + \ infty}$${\ Displaystyle а = - \ infty}$

Выражение не является неопределенной формой. Выражение, полученное в результате рассмотрения, дает предел , при условии, что он остается неотрицательным по мере приближения . Выражение аналогично : если as приближается , предел выходит как . ${\ displaystyle 0 ^ {\ infty}}$${\ displaystyle 0 ^ {+ \ infty}}$${\ Displaystyle \ lim _ {х \ к с} е (х) ^ {г (х)}}$${\ displaystyle 0 ~}$${\ displaystyle f (x)}$${\ displaystyle x}$${\ displaystyle c}$${\ displaystyle 0 ^ {- \ infty}}$${\ displaystyle 1/0}$${\ displaystyle f (x)> 0}$${\ displaystyle x}$${\ displaystyle c}$${\ displaystyle + \ infty}$

Чтобы понять, почему, позвольте where и Взяв натуральный логарифм обеих сторон и используя, мы получим то, что означает, что${\ Displaystyle L = \ lim _ {х \ к с} е (х) ^ {г (х)},}$${\ Displaystyle \ lim _ {х \ к с} {е (х)} = 0,}$${\ displaystyle \ lim _ {x \ to c} {g (x)} = \ infty.}$${\ displaystyle \ lim _ {x \ to c} \ ln {f (x)} = - \ infty,}$${\ displaystyle \ ln L = \ lim _ {x \ to c} ({g (x)} \ times \ ln {f (x)}) = \ infty \ times {- \ infty} = - \ infty,}$${\ displaystyle L = {e} ^ {- \ infty} = 0.}$

Оценка неопределенных форм

Прилагательное неопределенного вовсе не означает , что предел не существует, так как многие из приведенных выше примеров показывают. Во многих случаях можно использовать алгебраическое исключение, правило Л'Опиталя или другие методы для управления выражением, чтобы можно было оценить предел.

Эквивалент бесконечно малой

Когда две переменные и сходятся к нулю в одной и той же предельной точке и , они называются эквивалентными бесконечно малыми (эквивалентными ). ${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle \ textstyle \ lim {\ frac {\ beta} {\ alpha}} = 1}$${\ Displaystyle \ альфа \ сим \ бета}$

Более того, если переменные и таковы, что и , то: ${\ displaystyle \ alpha '}$${\ displaystyle \ beta '}$${\ Displaystyle \ альфа \ сим \ альфа '}$${\ displaystyle \ beta \ sim \ beta '}$

Вот краткое доказательство:

Предположим, есть две эквивалентные бесконечно малые и . ${\ Displaystyle \ альфа \ сим \ альфа '}$${\ displaystyle \ beta \ sim \ beta '}$

${\ displaystyle \ lim {\ frac {\ beta} {\ alpha}} = \ lim {\ frac {\ beta \ beta '\ alpha'} {\ beta '\ alpha' \ alpha}} = \ lim {\ frac {\ beta} {\ beta '}} \ lim {\ frac {\ alpha'} {\ alpha}} \ lim {\ frac {\ beta '} {\ alpha'}} = \ lim {\ frac {\ beta '} {\ alpha'}}}$

Для оценки неопределенной формы можно использовать следующие факты об эквивалентных бесконечно малых (например, если x становится ближе к нулю): ${\ displaystyle 0/0}$${\ Displaystyle х \ сим \ грех х}$

Например:

${\ displaystyle {\ begin {align} \ lim _ {x \ to 0} {\ frac {1} {x ^ {3}}} \ left [\ left ({\ frac {2+ \ cos x} {3 }} \ right) ^ {x} -1 \ right] & = \ lim _ {x \ to 0} {\ frac {e ^ {x \ ln {\ frac {2+ \ cos x} {3}}} -1} {x ^ {3}}} \\ & = \ lim _ {x \ to 0} {\ frac {1} {x ^ {2}}} \ ln {\ frac {2+ \ cos x} {3}} \\ & = \ lim _ {x \ to 0} {\ frac {1} {x ^ {2}}} \ ln \ left ({\ frac {\ cos x-1} {3}} +1 \ right) \\ & = \ lim _ {x \ to 0} {\ frac {\ cos x-1} {3x ^ {2}}} \\ & = \ lim _ {x \ to 0} - {\ frac {x ^ {2}} {6x ^ {2}}} \\ & = - {\ frac {1} {6}} \ end {выровнено}}}$

Во 2 - ^м равенства, где , как у стали ближе к 0 , используется, и где используется в 4 - ^е равенство, и используется в 5 - ^й равенства. ${\ displaystyle e ^ {y} -1 \ sim y}$${\ Displaystyle у = х \ пер {2+ \ соз х \ более 3}}$${\ Displaystyle у \ сим \ ln {(1 + y)}}$${\ Displaystyle у = {{\ соз х-1} \ более 3}}$${\ Displaystyle 1- \ соз х \ сим {х ^ {2} \ более 2}}$

Правило L'Hôpital

Правило L'Hôpital - это общий метод оценки неопределенных форм и . Это правило гласит, что (при соответствующих условиях) ${\ displaystyle 0/0}$${\ displaystyle \ infty / \ infty}$

где и - производные от и . (Обратите внимание, что это правило не применяется к выражениям , и так далее, поскольку эти выражения не являются неопределенными формами.) Эти производные позволят выполнить алгебраическое упрощение и, в конечном итоге, оценить предел. ${\ displaystyle f '}$${\ displaystyle g '}$${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle \ infty / 0}$${\ displaystyle 1/0}$

Правило Л'Опиталя может также применяться к другим неопределенным формам, используя сначала соответствующее алгебраическое преобразование. Например, чтобы оценить форму 0 ⁰ :

Правая часть имеет форму , поэтому к ней применимо правило L'Hôpital. Обратите внимание, что это уравнение действительно (пока определена правая часть), потому что натуральный логарифм (ln) является непрерывной функцией ; не имеет значения, насколько хорошо он себя ведет, и может (или не может) быть, пока асимптотически положителен. (область логарифмов - это набор всех положительных действительных чисел.) ${\ displaystyle \ infty / \ infty}$${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle f}$

Хотя правило L'Hôpital применяется к обоим и , одна из этих форм может быть более полезной, чем другая в конкретном случае (из-за возможности алгебраического упрощения впоследствии). При необходимости можно переключаться между этими формами, преобразовавшись в . ${\ displaystyle 0/0}$${\ displaystyle \ infty / \ infty}$${\ displaystyle f / g}$${\ Displaystyle (1 / г) / (1 / е)}$

Список неопределенных форм

В следующей таблице перечислены наиболее распространенные неопределенные формы и преобразования для применения правила Л'Опиталя.

Неопределенная форма	Условия	Преобразование в ${\ displaystyle 0/0}$	Преобразование в ${\ displaystyle \ infty / \ infty}$
0/0	${\ Displaystyle \ lim _ {х \ к с} е (х) = 0, \ \ lim _ {х \ к с} г (х) = 0 \!}$	-	${\ displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to c} {\ frac {1 / g (x)} { 1 / f (x)}} \!}$
${\ displaystyle \ infty}$/${\ displaystyle \ infty}$	${\ Displaystyle \ lim _ {х \ к с} е (х) = \ infty, \ \ lim _ {х \ к с} г (х) = \ infty \!}$	${\ displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to c} {\ frac {1 / g (x)} { 1 / f (x)}} \!}$	-
${\ displaystyle 0 \ cdot \ infty}$	${\ displaystyle \ lim _ {x \ to c} е (x) = 0, \ \ lim _ {x \ to c} g (x) = \ infty \!}$	${\ displaystyle \ lim _ {x \ to c} f (x) g (x) = \ lim _ {x \ to c} {\ frac {f (x)} {1 / g (x)}} \! }$	${\ displaystyle \ lim _ {x \ to c} f (x) g (x) = \ lim _ {x \ to c} {\ frac {g (x)} {1 / f (x)}} \! }$
${\ displaystyle \ infty - \ infty}$	${\ Displaystyle \ lim _ {х \ к с} е (х) = \ infty, \ \ lim _ {х \ к с} г (х) = \ infty \!}$	${\ Displaystyle \ lim _ {х \ к с} (е (х) -g (х)) = \ lim _ {х \ к с} {\ гидроразрыва {1 / г (х) -1 / f (х) } {1 / (f (x) g (x))}} \!}$	${\ displaystyle \ lim _ {x \ to c} (f (x) -g (x)) = \ ln \ lim _ {x \ to c} {\ frac {e ^ {f (x)}} {е ^ {g (x)}}} \!}$
${\ displaystyle 0 ^ {0}}$	${\ displaystyle \ lim _ {x \ to c} f (x) = 0 ^ {+}, \ lim _ {x \ to c} g (x) = 0 \!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {g (x)} {1 / \ ln f (Икс)}}\!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {\ ln f (x)} {1 / g (Икс)}}\!}$
${\ displaystyle 1 ^ {\ infty}}$	${\ Displaystyle \ lim _ {х \ к с} е (х) = 1, \ \ lim _ {х \ до с} г (х) = \ infty \!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {\ ln f (x)} {1 / g (Икс)}}\!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {g (x)} {1 / \ ln f (Икс)}}\!}$
${\ displaystyle \ infty ^ {0}}$	${\ displaystyle \ lim _ {x \ to c} е (x) = \ infty, \ \ lim _ {x \ to c} g (x) = 0 \!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {g (x)} {1 / \ ln f (Икс)}}\!}$	${\ displaystyle \ lim _ {x \ to c} f (x) ^ {g (x)} = \ exp \ lim _ {x \ to c} {\ frac {\ ln f (x)} {1 / g (Икс)}}\!}$

Смотрите также

• Определенный и неопределенный
• Деление на ноль
• Расширенная строка действительных чисел
• Неопределенное уравнение
• Неопределенная система
• Неопределенный (переменный)
• Правило L'Hôpital

использованная литература