Механика движения плоских частиц - Mechanics of planar particle motion

Часть серии о
Классическая механика
${\ displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (м {\ textbf {v}})}$ Второй закон движения
История Лента новостей Учебники
ветви
Основы
Составы
Основные темы
Вращение
Ученые
Физический портал  Категория
v т е

В этой статье описывается плоское движение частицы при наблюдении из неинерциальных систем отсчета . Наиболее известные примеры плоского движения связаны с движением двух сфер, гравитационно притягивающихся друг к другу, и обобщением этой проблемы на движение планет . См. Центробежную силу , проблему двух тел , орбиту и законы движения планет Кеплера . Эти проблемы относятся к общей области аналитической динамики , определения орбит по заданным законам силы. В этой статье больше внимания уделяется кинематическим вопросам, связанным с плоским движением, то есть определению сил, необходимых для достижения определенной траектории с учетом траектории частицы. Общие результаты, представленные здесь в фиктивных силах , применяются к наблюдениям за движущейся частицей, видимой из нескольких конкретных неинерциальных систем, например, локальной системы (одна привязана к движущейся частице, поэтому она кажется неподвижной) и совместно вращающейся системы отсчета. (один с произвольно расположенной, но фиксированной осью и скоростью вращения, при которой кажется, что частица имеет только радиальное движение и нулевое азимутальное движение). Вводится лагранжев подход к фиктивным силам.

В отличие от реальных сил, таких как электромагнитные силы , фиктивные силы не возникают в результате физического взаимодействия между объектами.

Анализ с использованием фиктивных сил

Появление фиктивных сил обычно связано с использованием неинерциальной системы отсчета , а их отсутствие - с использованием инерциальной системы отсчета . Связь между инерциальными системами отсчета и фиктивными силами (также называемыми силами инерции или псевдосилами ) выражена, например, Арнольдом:

Уравнения движения в неинерциальной системе отличаются от уравнений в инерциальной системе дополнительными членами, называемыми силами инерции. Это позволяет нам экспериментально обнаружить неинерциальный характер системы.

-  В.И. Арнольд: Математические методы классической механики, второе издание, с. 129

Иро предлагает несколько иную точку зрения на эту тему:

Дополнительная сила из-за неоднородного относительного движения двух систем отсчета называется псевдосилой .

-  Хиро в современном подходе к классической механике с. 180

Фиктивные силы не появляются в уравнениях движения в инерциальной системе отсчета : в инерциальной системе отсчета движение объекта объясняется реальными приложенными силами. Однако в неинерциальной системе отсчета, такой как вращающаяся, первый и второй законы Ньютона по-прежнему могут использоваться для точных физических предсказаний при условии, что вместе с реальными силами учтены фиктивные силы. Для решения задач механики в неинерциальных системах отсчета в учебниках советуют относиться к фиктивным силам как к реальным силам и притворяться, что вы находитесь в инерциальной системе отсчета.

Относитесь к фиктивным силам как к реальным силам и притворяйтесь, что вы находитесь в инерциальной системе отсчета.

-  Луи Н. Хэнд, Джанет Д. Финч Аналитическая механика , с. 267

Следует отметить, что «рассмотрение фиктивных сил как реальных сил» означает, в частности, что фиктивные силы, видимые в конкретной неинерциальной системе отсчета, трансформируются как векторы при преобразованиях координат, выполненных в этой системе координат, то есть как реальные силы.

Движущиеся объекты и системы наблюдения

Затем было замечено, что меняющиеся во времени координаты используются как в инерциальной, так и в неинерциальной системе отсчета, поэтому использование изменяющихся во времени координат не следует путать со сменой наблюдателя, а является лишь изменением выбора наблюдателем описания. . Подробное описание этого пункта и несколько цитат по этому поводу.

Система отсчета и система координат

Термин система отсчета часто используется в очень широком смысле, но для настоящего обсуждения его значение ограничено для обозначения состояния движения наблюдателя , то есть либо инерциальной системы отсчета, либо неинерциальной системы отсчета. .

Термин « система координат» используется для различения различных возможных вариантов набора переменных для описания движения, выбора, доступного любому наблюдателю, независимо от его состояния движения. Примерами являются декартовы координаты , полярные координаты и (в более общем смысле) криволинейные координаты .

Вот две цитаты, относящиеся к «состоянию движения» и «системе координат»:

Сначала мы вводим понятие системы отсчета , которое само по себе связано с идеей наблюдателя : система отсчета в некотором смысле является «евклидовым пространством, переносимым наблюдателем». Дадим более математическое определение:… система отсчета - это… множество всех точек в евклидовом пространстве с движением твердого тела наблюдателя. Рама, обозначается , как говорят, двигаться вместе с наблюдателем. ... пространственные положения частиц обозначены по отношению к раме путем создания системы координат R с началом O . Соответствующий набор осей, разделяющих движение твердого тела рамы , можно рассматривать как физическую реализацию . В кадре координаты изменяются с R на R ' путем выполнения в каждый момент времени того же преобразования координат компонентов внутренних объектов (векторов и тензоров), вводимых для представления физических величин в этом кадре .${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$ ${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$

-  Жан Саленсон, Стивен Лайл. (2001). Справочник по механике сплошной среды: общие понятия, термоупругость с. 9

В традиционных разработках специальной и общей теории относительности было принято не различать две совершенно разные идеи. Первое - это понятие системы координат, понимаемое просто как плавное, обратимое присвоение четырех чисел событиям в окрестностях пространства-времени. Вторая, система отсчета, относится к идеализированной системе, используемой для присвоения таких чисел ... Чтобы избежать ненужных ограничений, мы можем отделить это расположение от метрических понятий. … Для наших целей особенно важно то, что каждая система отсчета имеет определенное состояние движения в каждом событии пространства-времени… В контексте специальной теории относительности и до тех пор, пока мы ограничиваемся системами отсчета при инерционном движении, тогда мало из важность зависит от разницы между инерциальной системой отсчета и инерциальной системой координат, которую она создает. Это удобное обстоятельство исчезает сразу же, как только мы начинаем рассматривать системы отсчета в неравномерном движении даже в рамках специальной теории относительности ... понятие системы отсчета вновь появилось как структура, отличная от системы координат.

-  Джон Д. Нортон: Общая ковариация и основы общей теории относительности: восемь десятилетий споров , Rep. Prog. Phys. , 56 , с. 835-7.

Системы координат, меняющиеся во времени

В общей системе координат базисные векторы для координат могут изменяться во времени в фиксированных положениях, или они могут изменяться в зависимости от положения в фиксированные моменты времени, или и то, и другое. Можно отметить, что системы координат, прикрепленные как к инерциальным кадрам, так и к неинерциальным кадрам, могут иметь базисные векторы, которые изменяются во времени, пространстве или обоих, например, описание траектории в полярных координатах, как видно из инерциальной системы отсчета. или если смотреть со стороны вращающейся рамы. Зависящее от времени описание наблюдений не меняет систему отсчета, в которой наблюдения производятся и записываются.

Фиктивные силы в локальной системе координат

Рисунок 1: Локальная система координат для плоского движения по кривой. Для расстояний s и s + ds вдоль кривой показаны два разных положения . В каждой позиции s единичный вектор u _n указывает вдоль внешней нормали к кривой, а единичный вектор u _t является касательным к траектории. Радиус кривизны траектории равен ρ, определяемой из скорости вращения касательной к кривой относительно длины дуги, и представляет собой радиус соприкасающейся окружности в позиции s . Единичный кружок слева показывает вращение единичных векторов с s .

При обсуждении частицы, движущейся по круговой орбите, в инерциальной системе отсчета можно выделить центростремительные и тангенциальные силы. Тогда, кажется, не проблема сменить шляпу, изменить перспективу и поговорить о фиктивных силах, обычно называемых центробежной силой и силой Эйлера . Но то, что лежит в основе этого переключения в словарном запасе, - это смена системы отсчета наблюдений с инерциальной системы отсчета, с которой мы начали, где центростремительные и тангенциальные силы имеют смысл, на вращающуюся систему отсчета, в которой частица кажется неподвижной, а центробежные фиктивные силы и силы Эйлера должны изменяться. быть вовлеченным в игру. Этот переключатель бессознательный, но настоящий.

Предположим, мы сидим на частице в общем плоском движении (а не только по круговой орбите). Какой анализ лежит в основе смены шляп при введении фиктивных центробежных сил и сил Эйлера?

Чтобы изучить этот вопрос, начните с инерциальной системы отсчета. Используя систему координат, обычно используемую при плоском движении, так называемую локальную систему координат , как показано на рисунке 1 , становится легко определить формулы для центростремительной внутренней силы, перпендикулярной траектории (в направлении, противоположном u _n на рисунке 1). ) и касательной силы, параллельной траектории (в направлении u _t ), как показано ниже.

Чтобы ввести единичные векторы локальной системы координат, показанной на рисунке 1 , можно начать с декартовых координат в инерциальной системе координат и описать локальные координаты в терминах этих декартовых координат. На рисунке 1 , то длина дуги s является расстоянием частицы объездила вдоль его путей во время т . Путь r ( t ) с компонентами x ( t ), y ( t ) в декартовых координатах описывается с использованием длины дуги s ( t ) как:

${\ Displaystyle \ mathbf {r} (s) = \ left [x (s), \ y (s) \ right] \.}$

Длина дуги s (t) измеряет расстояние по следу небесного писателя. Изображение из НАСА ASRS

Один из способов взглянуть на использование s - представить себе путь частицы как сидящую в пространстве, как след, оставленный небесным писателем , независимо от времени. Любая позиция на этом пути описывается указанием расстояния s от некоторой начальной точки пути. Тогда инкрементное смещение по пути ds описывается следующим образом:

${\ displaystyle d \ mathbf {r} (s) = \ left [dx (s), \ dy (s) \ right] = \ left [x '(s), \ y' (s) \ right] ds \ ,}$

где штрихи введены для обозначения производных по s . Величина этого смещения равна ds , что показывает, что:

${\ displaystyle \ left [x '(s) ^ {2} + y' (s) ^ {2} \ right] = 1 \.}$    (Уравнение 1)

Это смещение обязательно касается кривой в точке s , показывая, что касательный к кривой единичный вектор равен:

${\ displaystyle \ mathbf {u} _ {t} (s) = \ left [x '(s), \ y' (s) \ right] \,}$

в то время как направленный наружу единичный вектор, нормальный к кривой, равен

${\ displaystyle \ mathbf {u} _ {n} (s) = \ left [y '(s), \ -x' (s) \ right] \,}$

Ортогональность можно проверить, показав, что скалярное произведение вектора равно нулю. Единичная величина этих векторов является следствием уравнения. 1 .

Кроме того, обратите внимание, что использование единичных векторов, которые не выровнены по декартовой оси xy , не означает, что мы больше не находимся в инерциальной системе отсчета. Все это означает, что мы используем единичные векторы, которые меняются в зависимости от s, для описания пути, но по-прежнему наблюдаем движение из инерциальной системы отсчета.

Используя касательный вектор, угол касательной к кривой, скажем θ, определяется по формуле:

${\ displaystyle \ sin \ theta = {\ frac {y '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = y' (s) \;}$   а также   ${\ displaystyle \ cos \ theta = {\ frac {x '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = x' (s) \.}$

Радиус кривизны вводится совершенно формально (без геометрической интерпретации) как:

${\ displaystyle {\ frac {1} {\ rho}} = {\ frac {d \ theta} {ds}} \.}$

Производная от θ может быть найдена из производной sin θ:

${\ displaystyle {\ frac {d \ sin \ theta} {ds}} = \ cos \ theta {\ frac {d \ theta} {ds}} = {\ frac {1} {\ rho}} \ cos \ theta \}$

${\ displaystyle = {\ frac {1} {\ rho}} x '(s) \.}$

Теперь:

${\ displaystyle {\ frac {d \ sin \ theta} {ds}} = {\ frac {d} {ds}} {\ frac {y '(s)} {\ sqrt {x' (s) ^ {2 } + y ^ {2}}}}}$  ${\ displaystyle = {\ frac {y '' (s) x '(s) ^ {2} -y' (s) x '(s) x' '(s)} {\ left (x' (s) ^ {2} + y '(s) ^ {2} \ right) ^ {3/2}}} \,}$

в котором знаменатель равен единице согласно формуле. 1 . С помощью этой формулы для производной синуса радиус кривизны становится:

${\ displaystyle {\ frac {d \ theta} {ds}} = {\ frac {1} {\ rho}} = y '' (s) x '(s) -y' (s) x '' (s) ) \}$ ${\ displaystyle = {\ frac {y '' (s)} {x '(s)}} = - {\ frac {x' '(s)} {y' (s)}} \,}$

где эквивалентность форм проистекает из дифференцирования уравнения. 1 :

${\ displaystyle x '(s) x' '(s) + y' (s) y '' (s) = 0 \.}$

Установив описание любой позиции на пути в терминах связанного с ним значения s и найдя свойства пути в терминах этого описания, движение частицы вводится путем определения положения частицы в любой момент времени t как соответствующее значение s (t) .

Используя приведенные выше результаты для свойств траектории в единицах s , ускорение в инерциальной системе отсчета, описанное в терминах нормальных и касательных к траектории частицы компонентов, может быть найдено в терминах функции s ( t ) и ее различные производные по времени (как и раньше, штрихи обозначают дифференциацию по s ):

${\ displaystyle \ mathbf {a} (s) = {\ frac {d} {dt}} \ mathbf {v} (s)}$  ${\ displaystyle = {\ frac {d} {dt}} \ left [{\ frac {ds} {dt}} \ left (x '(s), \ y' (s) \ right) \ right] \}$

${\ displaystyle = \ left ({\ frac {d ^ {2} s} {dt ^ {2}}} \ right) \ mathbf {u} _ {t} (s) + \ left ({\ frac {ds } {dt}} \ right) ^ {2} \ left (x '' (s), \ y '' (s) \ right)}$

${\ displaystyle = \ left ({\ frac {d ^ {2} s} {dt ^ {2}}} \ right) \ mathbf {u} _ {t} (s) - \ left ({\ frac {ds } {dt}} \ right) ^ {2} {\ frac {1} {\ rho}} \ mathbf {u} _ {n} (s) \,}$

что можно проверить, взяв скалярное произведение с единичными векторами u _t ( s ) и u _n ( s ). Этот результат для ускорения такой же, как и для кругового движения на основе радиуса ρ. Используя эту систему координат в инерциальной системе отсчета, легко идентифицировать силу, нормальную к траектории, как центростремительную силу, а силу, параллельную траектории, как тангенциальную силу.

Далее мы меняем рамки наблюдения. Сидя на частице, мы принимаем неинерциальную систему отсчета, в которой частица находится в состоянии покоя (нулевая скорость). Эта система отсчета имеет непрерывно изменяющуюся точку отсчета, которая в момент времени t является центром кривизны (центром соприкасающегося круга на рисунке 1 ) пути в момент времени t , и скорость вращения которой является угловой скоростью движения частицы вокруг это происхождение в момент времени t . В этой неинерциальной системе отсчета также используются единичные векторы, нормальные к траектории и параллельные ей.

Угловая скорость этого кадра угловая скорость частицы относительно центра кривизны в момент времени т . Центростремительная сила инерциальной системы отсчета интерпретируется в неинерциальной системе отсчета, где тело находится в состоянии покоя, как сила, необходимая для преодоления центробежной силы. Точно так же сила, вызывающая любое ускорение скорости на пути, видимом в инерциальной системе отсчета, становится силой, необходимой для преодоления силы Эйлера в неинерциальной системе отсчета, где частица находится в состоянии покоя. В кадре отсутствует сила Кориолиса, потому что частица имеет нулевую скорость в этой системе отсчета. Например, для пилота самолета эти фиктивные силы являются предметом непосредственного опыта. Однако эти фиктивные силы не могут быть связаны с простой системой отсчета наблюдений, кроме самой частицы, если только она не движется по особенно простому пути, например, по кругу.

Тем не менее, с качественной точки зрения, траектория самолета может быть аппроксимирована дугой окружности в течение ограниченного времени, и в течение ограниченного времени применяется определенный радиус кривизны, центробежные силы и силы Эйлера могут быть проанализированы на основе кругового движения с этим радиусом. См. Статью о повороте самолета .

Далее более подробно рассматриваются опорные кадры, вращающиеся вокруг фиксированной оси.

Фиктивные силы в полярных координатах

Описание движения частицы часто проще в недекартовых системах координат, например в полярных координатах. Когда уравнения движения выражаются в терминах любой криволинейной системы координат, появляются дополнительные члены, которые представляют, как изменяются базисные векторы при изменении координат. Эти термины автоматически возникают на трансформацию в полярные (или цилиндрические) координаты и, таким образом , не фиктивные силы , а скорее просто добавляются условиями в ускорении в полярных координатах.

Две терминологии

При чисто математической трактовке, независимо от системы координат, с которой связана система координат (инерциальная или неинерциальная), при использовании криволинейных координат в ускорении наблюдаемой частицы появляются дополнительные члены. Например, в полярных координатах ускорение определяется выражением (подробности см. Ниже):

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d {\ boldsymbol {v}}} {dt}} = {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2} }} = ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

который содержит не только двойные производные координат по времени, но и дополнительные члены. В этом примере используются полярные координаты, но в более общем плане добавляемые термины зависят от того, какая система координат выбрана (то есть полярная, эллиптическая или что-то еще). Иногда эти термины, зависящие от системы координат, также упоминаются как «фиктивные силы», вводя второе значение для «фиктивных сил», несмотря на то, что эти термины не обладают свойствами преобразования вектора, ожидаемыми от сил. Например, см. Шанкар и Хильдебранд. Согласно этой терминологии, фиктивные силы частично определяются самой системой координат, независимо от системы координат, к которой она прикреплена, то есть независимо от того, привязана ли система координат к инерциальной или неинерциальной системе отсчета. Напротив, фиктивные силы, определенные в терминах состояния движения наблюдателя, исчезают в инерциальных системах отсчета. Чтобы различать эти две терминологии, фиктивные силы, исчезающие в инерциальной системе отсчета, силы инерции ньютоновской механики, называются в этой статье фиктивными силами «состояния движения» и те, которые возникают при интерпретации производных по времени. в частности системы координат называются «координатными» фиктивными силами.

Если предположить, что «состояние движения» и «система координат» различны , отсюда следует, что зависимость центробежной силы (как в этой статье) от «состояния движения» и ее независимость от «системы координат», что контрастирует с «координатная» версия с совершенно противоположными зависимостями указывает на то, что две разные идеи обозначаются терминологией «фиктивная сила». В данной статье подчеркивается одна из этих двух идей («состояние движения»), хотя описывается и другая.

Ниже полярные координаты вводятся для использования (сначала) в инерциальной системе отсчета, а затем (во-вторых) во вращающейся системе отсчета. Указываются на два различных использования термина «фиктивная сила». Однако сначала следует небольшое отступление, чтобы объяснить, как возникла терминология «координированной» фиктивной силы.

Лагранжев подход

Чтобы мотивировать введение «координированных» сил инерции не только ссылкой на «математическое удобство», ниже следует отступление, чтобы показать, что эти силы соответствуют тому, что некоторые авторы называют «обобщенными» фиктивными силами или «обобщенными силами инерции». Эти силы вводятся через подход лагранжевой механики к механике, основанный на описании системы с помощью обобщенных координат, обычно обозначаемых как { q _k }. Единственное требование к этим координатам состоит в том, что они необходимы и достаточны для однозначной характеристики состояния системы: они не обязательно должны быть (хотя могут быть) координатами частиц в системе. Вместо этого это могут быть углы и удлинения звеньев, например, в руке робота. Если механическая система состоит из N частиц и наложено m независимых кинематических условий, можно однозначно охарактеризовать систему с помощью n = 3 N - m независимых обобщенных координат { q _k }.

В классической механике лагранжиан определяется как кинетическая энергия , , системы минус ее потенциальной энергии , . В символах ${\ displaystyle T}$${\ displaystyle U}$

${\ Displaystyle L = TU. \ quad}$

В условиях, которые задаются в механике Лагранжа , если лагранжиан системы известен, то уравнения движения системы могут быть получены путем прямой подстановки выражения для лагранжиана в уравнение Эйлера – Лагранжа , конкретное семейство уравнения в частных производных .

Вот несколько определений:

Определение :

${\ Displaystyle L ({\ boldsymbol {q}}, \ {\ boldsymbol {\ dot {q}}}, \ t) = TU}$

- функция Лагранжа или лагранжиан , q _i - обобщенные координаты , - обобщенные скорости , ${\ displaystyle {\ dot {q_ {i}}}}$

${\ displaystyle \ partial L / \ partial {\ dot {q_ {i}}}}$   являются обобщенными импульсами ,

${\ displaystyle \ partial L / \ partial q_ {i}}$   являются обобщенными силами ,

${\ displaystyle {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {q_ {i}}}}}} - {\ frac {\ partial L} {\ partial q_ { i}}} = 0}$   являются уравнениями Лагранжа .

Мы не собираемся здесь описывать, как работает лагранжева механика. Заинтересованный читатель может посмотреть другие статьи, объясняющие этот подход. На данный момент цель состоит в том, чтобы просто показать, что лагранжев подход может привести к «обобщенным фиктивным силам», которые не исчезают в инерциальных системах отсчета . Здесь уместно то, что в случае отдельной частицы лагранжев подход может быть приспособлен для улавливания в точности только что введенных «координатных» фиктивных сил.

Чтобы продолжить, рассмотрим отдельную частицу и введем обобщенные координаты как { q _k } = ( r, θ ). Затем Хильдебранд показывает в полярных координатах с q _k = (r, θ) "обобщенные импульсы":

${\ displaystyle p_ {r} = m {\ dot {r}} \, \ p _ {\ theta} = mr ^ {2} {\ dot {\ theta}} \,}$

приводя, например, к обобщенной силе:

${\ displaystyle {\ frac {d} {dt}} p_ {r} = Q_ {r} + mr {\ dot {\ theta}} ^ {2} \,}$

где Q _r - приложенная радиальная сила. Связь между «обобщенными силами» и силами Ньютона зависит от выбора координат. Эта лагранжева формулировка вводит в точности упомянутую выше «координатную» форму фиктивных сил, которая допускает «фиктивные» (обобщенные) силы в инерциальных системах отсчета, например, термин « Внимательное прочтение» Хильдебранда показывает, что он не обсуждает роль «инерциальных систем координат». ссылка », и фактически говорит:« [Наличие] или отсутствие [сил инерции] зависит не от конкретной рассматриваемой проблемы, а от выбранной системы координат ». Под системой координат предположительно подразумевается выбор { q _k }. Позже он говорит: «Если ускорения, связанные с обобщенными координатами, должны представлять первостепенный интерес (как это обычно бывает), [неускоренные] члены могут быть удобно перенесены вправо ... и рассмотрены как дополнительные (обобщенные) силы инерции. Такие силы инерции часто говорят, что они относятся к типу Кориолиса ". ${\ Displaystyle г-н {\ точка {\ theta}} ^ {2} \.}$

Короче говоря, акцент некоторых авторов на координатах и ​​их производных и введение (обобщенных) фиктивных сил, которые не исчезают в инерциальных системах отсчета, является результатом использования обобщенных координат в лагранжевой механике . Например, см. Маккуарри Хильдебранд и фон Шверин. Ниже приведен пример такого использования в конструкции роботов-манипуляторов:

В приведенных выше уравнениях [Лагранжа-Эйлера] есть три типа членов. Первый включает в себя вторую производную от обобщенных координат. Второй квадратичный по отношению к коэффициентам, которые могут зависеть от . Далее они делятся на два типа. Термины, относящиеся к продукту этого типа , называются центробежными силами, а термины, относящиеся к продукту типа для i j , называются силами Кориолиса . Третий тип - это функции только и называются гравитационными силами .${\ displaystyle \ mathbf {\ dot {q}}}$${\ displaystyle \ mathbf {q}}$${\ Displaystyle {{\ точка {q}} _ {я}} ^ {2}}$${\ displaystyle {\ dot {q}} _ {i} {\ dot {q}} _ {j}}$${\ displaystyle \ mathbf {q}}$

-  Шужи С. Ге, Тонг Хенг Ли и Кристофер Джон Харрис: Адаптивное нейросетевое управление роботизированными манипуляторами , стр. 47-48.

Для робота-манипулятора уравнения могут быть записаны в форме с использованием символов Кристоффеля Γ _ijk (обсуждаемых ниже) как:

${\ displaystyle \ sum _ {j = 1} ^ {n} \ M_ {ij} ({\ boldsymbol {q}}) {\ ddot {q}} _ {j} + \ sum _ {j, k = 1 } ^ {n} \ Gamma _ {ijk} {\ dot {q}} _ {j} {\ dot {q}} _ {k} + {\ frac {\ partial V} {\ partial q_ {i}} } = \ Upsilon _ {i} \; i = 1, ..., n \,}$

где M - «матрица инерции манипулятора», V - потенциальная энергия, создаваемая гравитацией (например), и - обобщенные силы на суставе i . Таким образом, термины, включающие символы Кристоффеля, определяют термины «обобщенный центробежный» и «обобщенный кориолисовый». ${\ displaystyle \ Upsilon _ {i}}$

Введение обобщенных фиктивных сил часто осуществляется без уведомления и без указания слова «обобщенные». Такое неаккуратное использование терминологии ведет к бесконечной путанице, потому что эти обобщенные фиктивные силы, в отличие от стандартных фиктивных сил «состояния движения», не исчезают в инерциальных системах отсчета.

Полярные координаты в инерциальной системе отсчета

Вектор положения r всегда направлен радиально от начала координат.

Вектор скорости v , всегда касающийся траектории движения.

Вектор ускорения a , не параллельный радиальному движению, но смещенный угловым и кориолисовым ускорениями, не касательный к траектории, а смещенный центростремительным и радиальным ускорениями.

Кинематические векторы в плоских полярных координатах. Обратите внимание, что установка ограничена не 2-м пространством, а плоскостью в любом более высоком измерении.

Ниже показано ускорение частицы в инерциальной системе координат с использованием полярных координат. По определению, в инерциальной системе отсчета нет фиктивных сил "состояния движения". После этой презентации контрастирующая терминология «координированных» фиктивных сил представлена ​​и подвергнута критике на основе невекториального трансформирующего поведения этих «сил».

В инерциальной системе отсчета пусть будет вектором положения движущейся частицы. Его декартовы компоненты ( x , y ): ${\ displaystyle \ mathbf {r}}$

${\ Displaystyle \ mathbf {г} = (г \ соз \ тета, \ г \ грех \ тета) \,}$

с полярными координатами r и θ в зависимости от времени t .

Единичные векторы определены в радиальном направлении наружу : ${\ displaystyle \ mathbf {r}}$

${\ displaystyle {\ hat {\ boldsymbol {r}}} = {\ frac {\ partial \ mathbf {r}} {\ partial r}} = (\ cos \ theta, \ \ sin \ theta)}$

и в направлении под прямым углом к : ${\ displaystyle \ mathbf {r}}$

${\ displaystyle {\ hat {\ boldsymbol {\ theta}}} = {\ frac {\ partial ^ {2} {\ mathbf {r}}} {\ partial r \, \ partial \ theta}} = (- \ грех \ тета \, \ соз \ тета) \.}$

Эти единичные векторы меняются по направлению со временем:

${\ displaystyle {\ frac {d} {dt}} {\ hat {\ boldsymbol {r}}} = (- \ sin \ theta, \ \ cos \ theta) {\ frac {d \ theta} {dt}} = {\ frac {d \ theta} {dt}} {\ hat {\ boldsymbol {\ theta}}},}$

а также:

${\ displaystyle {\ frac {d} {dt}} {\ hat {\ boldsymbol {\ theta}}} = (- \ cos \ theta, \ - \ sin \ theta) {\ frac {d \ theta} {dt }} = - {\ frac {d \ theta} {dt}} {\ hat {\ boldsymbol {r}}}.}$

Используя эти производные, первая и вторая производные позиции:

${\ displaystyle {\ boldsymbol {v}} = {\ frac {d \ mathbf {r}} {dt}} = {\ dot {r}} {\ hat {\ boldsymbol {r}}} + r {\ dot {\ theta}} {\ hat {\ boldsymbol {\ theta}}},}$

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d {\ boldsymbol {v}}} {dt}} = {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2} }} = ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

где точечные отметки указывают на дифференциацию по времени. При такой форме ускорения в инерциальной системе отсчета второй закон Ньютона, выраженный в полярных координатах, имеет вид: ${\ displaystyle {\ boldsymbol {а}}}$

${\ displaystyle {\ boldsymbol {F}} = m {\ boldsymbol {a}} = m ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + m (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

где F - чистая реальная сила, действующая на частицу. Никаких фиктивных сил не возникает, потому что все фиктивные силы по определению равны нулю в инерциальной системе отсчета.

Однако с математической точки зрения иногда бывает удобно поместить только производные второго порядка в правую часть этого уравнения; то есть мы запишем приведенное выше уравнение, переставив термины как:

${\ displaystyle {\ boldsymbol {F}} + mr {\ dot {\ theta}} ^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta} }} {\ hat {\ boldsymbol {\ theta}}} = m {\ tilde {\ boldsymbol {a}}} = m {\ ddot {r}} {\ hat {\ boldsymbol {r}}} + mr { \ ddot {\ theta}} {\ hat {\ boldsymbol {\ theta}}} \,}$

где введен «координатный» вариант «ускорения»:

${\ displaystyle {\ tilde {\ boldsymbol {a}}} = {\ ddot {r}} {\ hat {\ boldsymbol {r}}} + r {\ ddot {\ theta}} {\ hat {\ boldsymbol { \ theta}}} \,}$

состоящий только из производных второго порядка по времени от координат r и θ. Члены, перенесенные в силовую сторону уравнения, теперь рассматриваются как дополнительные «фиктивные силы», и, что сбивает с толку, результирующие силы также называются «центробежной» и «кориолисовой» силой.

Эти вновь определенные «силы» не равны нулю в инерциальной системе отсчета и, таким образом, определенно не совпадают с ранее идентифицированными фиктивными силами, которые равны нулю в инерциальной системе отсчета и ненулевые только в неинерциальной системе отсчета. В этой статье эти недавно определенные силы называются «координатной» центробежной силой и «координатной» силой Кориолиса, чтобы отделить их от сил «состояния движения».

Рисунок 2: Две системы координат, отличающиеся смещением начала координат. Радиальное движение с постоянной скоростью v в одном кадре не является радиальным в другом. Угловая скорость , но ${\ displaystyle {\ dot {\ theta}} = 0}$${\ displaystyle {\ dot {\ theta}} '\ neq 0 \.}$

Изменение происхождения

Вот иллюстрация, показывающая, что так называемый «центробежный термин» не трансформируется как истинная сила, при этом любое упоминание этого термина не просто как «термин», а как центробежная сила в сомнительном свете. Предположим, что в системе S частица движется радиально от начала координат с постоянной скоростью. См. Рис. 2. Сила, действующая на частицу, равна нулю по первому закону Ньютона. Теперь мы посмотрим на то же самое из кадра S ' , который тот же, но смещен в начале координат. В S ' частица все еще движется по прямой с постоянной скоростью, так что сила снова равна нулю. ${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$

Что, если мы используем полярные координаты в двух кадрах? В системе S радиальное движение постоянно, угловое движение отсутствует. Следовательно, ускорение составляет:

${\ displaystyle {\ boldsymbol {a}} = \ left ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2} \ right) {\ hat {\ boldsymbol {r}}} + \ left (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}} \ right) {\ hat {\ boldsymbol {\ theta}}} = 0 \,}$

и каждый член в отдельности равен нулю, потому что и . В кадре S нет силы, в том числе и «силы» . Однако в кадре S ' мы имеем: ${\ Displaystyle {\ точка {\ theta}} = 0, \ {\ ddot {\ theta}} = 0}$${\ displaystyle {\ ddot {r}} = 0 \}$${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$

${\ displaystyle {\ boldsymbol {a}} '= \ left ({\ ddot {r}}' - r '{\ dot {\ theta}}' ^ {2} \ right) {\ hat {\ boldsymbol {r }}} '+ \ left (r' {\ ddot {\ theta}} '+ 2 {\ dot {r}}' {\ dot {\ theta}} '\ right) {\ hat {\ boldsymbol {\ theta }}} '\}$

В этом случае азимутальный член равен нулю и представляет собой скорость изменения углового момента. Однако для получения нулевого ускорения в радиальном направлении нам необходимы:

${\ displaystyle {\ ddot {r}} '= r' {\ dot {\ theta}} '^ {2} \.}$

Правая часть не равна нулю, поскольку ни ни равна нулю. То есть, мы не можем получить нулевую силу (ноль ), если сохраним только ускорение; нам нужны оба условия. ${\ displaystyle r '\}$${\ displaystyle {\ dot {\ theta}} '}$${\ Displaystyle {\ boldsymbol {а}} '\}$${\ displaystyle {\ ddot {r}} '}$

Несмотря на вышеизложенные факты, предположим, что мы принимаем полярные координаты и хотим сказать, что это «центробежная сила», и интерпретируем их как «ускорение» (не вдаваясь в какие-либо возможные обоснования). Как обстоит дело с этим решением, если учесть, что правильная формулировка физики не зависит от геометрии и координат? См. Статью об общей ковариации . Чтобы попытаться сформировать ковариантное выражение, эту так называемую центробежную «силу» можно записать в векторную запись как: ${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$${\ displaystyle {\ ddot {r}}}$

${\ displaystyle {\ boldsymbol {F _ {\ dot {\ theta}}}} = - {\ boldsymbol {\ omega \ times}} \ left ({\ boldsymbol {\ omega \ times r}} \ right) \,}$

с участием:

${\ displaystyle {\ boldsymbol {\ omega}} = {\ dot {\ theta}} {\ boldsymbol {\ hat {k}}} \,}$

и единичный вектор, нормальный к плоскости движения. К сожалению, хотя это выражение формально выглядит как вектор, когда наблюдатель меняет источник, значение изменений (см. Рисунок 2), поэтому наблюдатели в одной системе отсчета, стоящие на разных углах улицы, видят разные «силы», даже если фактические события они Свидетели идентичны. Как может физическая сила (фиктивная или реальная) быть равной нулю в одном кадре S , но ненулевой в другом кадре S ' идентичной, но на расстоянии нескольких футов? Даже для одного и того же поведения частицы выражение разное в каждой системе отсчета, даже для очень тривиальных различий между кадрами. Короче говоря, если принять за «центробежную силу», она не имеет универсального значения: она нефизична . ${\ displaystyle {\ boldsymbol {\ hat {k}}}}$${\ displaystyle {\ dot {\ theta}}}$${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$

Помимо этой проблемы, реальная сила воздействия равна нулю. (При прямолинейном движении с постоянной скоростью нет реальной приложенной силы). Если принять полярные координаты, и хочет сказать , что это «центробежная сила», и переосмысливать как «ускорение», результаты странности в рамке S» , что прямолинейное движение с постоянной скоростью требует результирующей силы в полярных координатах, но не в Декартовы координаты. Более того, эта растерянность применяется в рамке S ' , но не в кадре S . ${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$${\ displaystyle {\ ddot {r}}}$

Абсурдность поведения указывает на то, что нужно сказать, что это не центробежная сила , а просто одно из двух слагаемых ускорения. Эта точка зрения, что ускорение состоит из двух частей, не зависит от системы отсчета: центробежная сила равна нулю в любой системе отсчета инерции. Он также не зависит от системы координат: мы можем использовать декартову, полярную или любую другую криволинейную систему: все они дают ноль. ${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$${\ Displaystyle г {\ точка {\ theta}} ^ {2}}$

Помимо приведенных выше физических аргументов, конечно, приведенный выше вывод, основанный на применении математических правил дифференцирования, показывает, что радиальное ускорение действительно состоит из двух членов . ${\ displaystyle {\ ddot {r}} - r {\ dot {\ theta}} ^ {2}}$

Тем не менее, следующий подраздел показывает, что существует связь между этими центробежными и кориолисовыми членами и фиктивными силами, которые относятся к конкретной вращающейся системе отсчета (в отличие от инерциальной системы отсчета).

Рисунок 3: Инерциальная система отсчета S и мгновенная неинерциальная система отсчета S ', вращающаяся в одном направлении . Совместно вращающаяся рамка вращается с угловой скоростью Ω, равной скорости вращения частицы вокруг начала координат S ' в конкретный момент t . Частица расположена в позиции вектора r (t), и единичные векторы показаны в радиальном направлении к частице от начала координат, а также в направлении увеличения угла θ перпендикулярно радиальному направлению. Эти единичные векторы не обязательно должны быть связаны с касательной и нормалью к пути. Кроме того, радиальное расстояние r не обязательно должно быть связано с радиусом кривизны пути.

Совместно вращающаяся рама

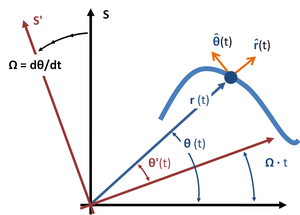
В случае плоского движения частицы «координатные» центробежные члены и члены кориолисова ускорения, найденные выше, отличные от нуля в инерциальной системе отсчета, могут быть показаны как отрицательные значения центробежных и кориолисовых членов «состояния движения». которые появляются в очень специфической неинерциальной системе одновременного вращения (см. следующий подраздел). См. Рисунок 3 . Чтобы определить совместно вращающуюся рамку, сначала выбирается исходная точка, от которой определяется расстояние r (t) до частицы. Устанавливается ось вращения, которая перпендикулярна плоскости движения частицы и проходит через это начало. Затем в выбранный момент t скорость вращения совместно вращающейся системы Ω выравнивается со скоростью вращения частицы вокруг этой оси dθ / dt . Совместно вращающаяся рамка применяется только на мгновение и должна постоянно изменяться по мере движения частицы. Для получения более подробной информации см. Полярные координаты, центробежные условия и термины Кориолиса .

Полярные координаты во вращающейся системе отсчета

Затем тот же подход используется для нахождения фиктивных сил (неинерциальной) вращающейся системы отсчета. Например, если вращающаяся полярная система координат принята для использования во вращающейся системе наблюдения, обе вращаются с одинаковой постоянной скоростью против часовой стрелки Ω, мы находим уравнения движения в этой системе следующим образом: радиальная координата во вращающейся системе координат равна принято за r , но угол θ 'во вращающейся системе отсчета изменяется со временем:

${\ displaystyle \ theta '= \ theta - \ Omega t \.}$

Как следствие,

${\ displaystyle {\ dot {\ theta}} '= {\ dot {\ theta}} - \ Omega \.}$

Подключаем этот результат к ускорению с использованием единичных векторов из предыдущего раздела:

${\ displaystyle {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2}}} = \ left [{\ ddot {r}} - r \ left ({\ dot {\ theta}}) '+ \ Omega \ right) ^ {2} \ right] {\ hat {\ mathbf {r}}} + \ left [r {\ ddot {\ theta}}' + 2 {\ dot {r}} \ left ({\ dot {\ theta}} '+ \ Omega \ right) \ right] {\ hat {\ boldsymbol {\ theta}}}}$

${\ displaystyle = ({\ ddot {r}} - r {\ dot {\ theta}} '^ {2}) {\ hat {\ mathbf {r}}} + (r {\ ddot {\ theta}} '+2 {\ dot {r}} {\ dot {\ theta}}') {\ hat {\ boldsymbol {\ theta}}} - \ left (2r \ Omega {\ dot {\ theta}} '+ r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} + \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}} \ .}$

Первые два члена имеют ту же форму, что и в инерциальной системе отсчета, и они являются единственными членами, если система не вращается, то есть если Ω = 0. Однако в этой вращающейся рамке у нас есть дополнительные термины:

${\ displaystyle - \ left (2r \ Omega {\ dot {\ theta}} '+ r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} + \ left (2 {\ dot { r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}$

Радиальный член Ω ² r представляет собой центробежную силу на единицу массы из-за вращения системы со скоростью Ω, а радиальный член представляет собой радиальную составляющую силы Кориолиса на единицу массы, где - тангенциальная составляющая скорости частицы, как видно на вращающаяся рама. Этот термин представляет собой так называемую азимутальную составляющую силы Кориолиса на единицу массы. Фактически, эти дополнительные термины могут быть использованы для измерения Ω и обеспечения теста, чтобы увидеть, вращается ли рамка, точно так же, как объяснено в примере вращения идентичных сфер . Если движение частицы может быть описано наблюдателем с использованием законов движения Ньютона без этих Ω-зависимых членов, наблюдатель находится в инерциальной системе отсчета, где Ω = 0. ${\ displaystyle 2r \ Omega {\ dot {\ theta}} '}$${\ displaystyle r {\ dot {\ theta}} '}$${\ displaystyle - \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}$

Эти «дополнительные члены» в ускорении частицы представляют собой фиктивные силы «состояния движения» для этой вращающейся системы координат, силы, вносимые вращением системы координат с угловой скоростью Ω.

Каковы «координатные» фиктивные силы в этой вращающейся системе отсчета? Как и раньше, предположим, что мы решили поместить только производные второго порядка по времени в правую часть закона Ньютона:

${\ displaystyle {\ boldsymbol {F}} + mr {\ dot {\ theta}} '^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta}} '{\ hat {\ boldsymbol {\ theta}}} + m \ left (2r \ Omega {\ dot {\ theta}}}' + r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} - m \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}}$ ${\ displaystyle = m {\ ddot {r}} {\ hat {\ mathbf {r}}} + mr {\ ddot {\ theta}} '\ {\ hat {\ boldsymbol {\ theta}}}}$ ${\ Displaystyle = м {\ тильда {\ boldsymbol {а}}}}$

Если для удобства мы выберем некое так называемое «ускорение», тогда к так называемой «фиктивной силе» будут добавлены термины , которые не являются фиктивными силами «состояния движения», а на самом деле являются компонентами силы. которые сохраняются даже при Ω = 0, то есть сохраняются даже в инерциальной системе отсчета. Поскольку эти дополнительные члены добавлены, «координатная» фиктивная сила не совпадает с фиктивной силой «состояние движения». Из-за этих дополнительных условий «координатная» фиктивная сила не равна нулю даже в инерциальной системе отсчета. ${\ displaystyle {\ tilde {\ boldsymbol {a}}}}$${\ displaystyle (mr {\ dot {\ theta}} '^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta}}' {\ hat {\ boldsymbol {\ theta}}})}$

Подробнее о вращающейся в одном направлении раме

Обратите внимание, однако, на случай вращающейся системы отсчета, которая имеет ту же угловую скорость, что и частица, так что Ω = dθ / dt в некоторый конкретный момент (то есть полярные координаты устанавливаются в мгновенной неинерциальной координате -вращающаяся рамка рисунка 3 ). В этом случае в этот момент dθ '/ dt = 0 . В этой совместно вращающейся неинерциальной системе отсчета в этот момент «координатные» фиктивные силы - это только силы, обусловленные движением системы, то есть они такие же, как фиктивные силы «состояния движения», как обсуждалось. в замечаниях о вращающейся в одном направлении раме на Рисунке 3 в предыдущем разделе.

Фиктивные силы в криволинейных координатах

Рисунок 4: Координатные поверхности, координатные линии и координатные оси общих криволинейных координат.

Процитируем Булло и Льюиса: «Только в исключительных обстоятельствах конфигурация лагранжевой системы может быть описана вектором в векторном пространстве. В естественных математических условиях конфигурационное пространство системы описывается в общих чертах как искривленное пространство или, точнее, как дифференцируемое многообразие ".

Вместо декартовых координат , когда уравнения движения выражаются в криволинейной системе координат , символы Кристоффеля появляются в ускорении частицы, выраженном в этой системе координат, как более подробно описано ниже. Рассмотрим описание движения частицы с точки зрения инерциальной системы отсчета в криволинейных координатах. Предположим , что положение точки Р в декартовых координатах ( х , у , г ) и в криволинейных координатах ( д ₁ , д ₂ . Д ₃ ). Затем существуют функции, которые связывают эти описания:

${\ Displaystyle х = х (q_ {1}, \ q_ {2}, \ q_ {3}) \;}$ ${\ Displaystyle \ q_ {1} = q_ {1} (х, \ y, \ z) \,}$

и так далее. (Количество измерений может быть больше трех.) Важным аспектом таких систем координат является элемент длины дуги, который позволяет определять расстояния. Если криволинейные координаты образуют ортогональную систему координат , элемент длины дуги ds выражается как:

${\ displaystyle ds ^ {2} = \ sum _ {k = 1} ^ {d} \ left (h_ {k} \ right) ^ {2} \ left (dq_ {k} \ right) ^ {2} \ ,}$

где величины h _k называются масштабными факторами . Изменение dq _k в q _k вызывает смещение h _k dq _k вдоль координатной линии для q _k . В точке P поместим единичные векторы e _k, каждый из которых касается координатной линии переменной q _k . Тогда любой вектор может быть выражен в терминах этих базисных векторов, например, из инерциальной системы отсчета вектор положения движущейся частицы r, находящейся в момент времени t в позиции P, принимает следующий вид:

${\ displaystyle {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} q_ {k} \ {\ boldsymbol {e_ {k}}} \,}$

где Q _к есть вектор скалярное произведение из г и е _к . Скорость v частицы в точке P может быть выражена в точке P как:

${\ displaystyle {\ boldsymbol {v}} = \ sum _ {k = 1} ^ {d} v_ {k} \ {\ boldsymbol {e_ {k}}} \,}$

${\ displaystyle = {\ frac {d} {dt}} {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol { e_ {k}}} + \ sum _ {k = 1} ^ {d} q_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}} \,}$

где v _к вектор скалярное произведение в об и е _к и над точками указывают дифференцирование по времени. Производные по времени от базисных векторов могут быть выражены с помощью введенных выше масштабных коэффициентов. Например:

${\ displaystyle {\ frac {\ partial} {\ partial q_ {2}}} {\ boldsymbol {e_ {1}}} = - {\ boldsymbol {e}} _ {2} {\ frac {1} {h_ {2}}} {\ frac {\ partial h_ {1}} {\ partial q_ {2}}} - {\ boldsymbol {e}} _ {3} {\ frac {1} {h_ {3}}} {\ frac {\ partial h_ {1}} {\ partial q_ {3}}} \,}$  или вообще ${\ displaystyle {\ frac {\ partial {\ boldsymbol {e_ {j}}}} {\ partial q_ {k}}} = \ sum _ {n = 1} ^ {d} {\ Gamma ^ {n}} _ {kj} {\ boldsymbol {e_ {n}}} \,}$

в котором коэффициенты единичных векторов являются символами Кристоффеля для системы координат. Общие обозначения и формулы для символов Кристоффеля:

${\ displaystyle {\ Gamma ^ {i}} _ {ii} = {\ begin {Bmatrix} \, i \, \\ i \, \, i \ end {Bmatrix}} = {\ frac {1} {h_ {i}}} {\ frac {\ partial h_ {i}} {\ partial q_ {i}}} \! \; \}$ ${\ displaystyle {\ Gamma ^ {i}} _ {ij} = \ {\ begin {Bmatrix} \, i \, \\ i \, \, j \ end {Bmatrix}} = {\ frac {1} { h_ {i}}} {\ frac {\ partial h_ {i}} {\ partial q_ {j}}} = {\ begin {Bmatrix} \, i \, \\ j \, \, i \ end {Bmatrix }} \! \; \}$ ${\ displaystyle {\ Gamma ^ {j}} _ {ii} = {\ begin {Bmatrix} \, j \, \\ i \, \, i \ end {Bmatrix}} = - {\ frac {h_ {i }} {{h_ {j}} ^ {2}}} {\ frac {\ partial h_ {i}} {\ partial q_ {j}}} \,}$

и символ равен нулю, когда все индексы разные. Несмотря на кажущуюся противоположность, символы Кристоффеля не образуют компонентов тензора . Например, они равны нулю в декартовых координатах, но не в полярных координатах.

Используя отношения, подобные этому,

${\ displaystyle {\ dot {\ boldsymbol {e_ {j}}}} = \ sum _ {k = 1} ^ {d} {\ frac {\ partial} {\ partial q_ {k}}} {\ boldsymbol { е_ {j}}} {\ dot {q}} _ {k} \}$

${\ displaystyle = \ sum _ {k = 1} ^ {d} \ sum _ {i = 1} ^ {d} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i } {\ boldsymbol {e_ {k}}} \,}$

что позволяет оценить все производные по времени. Например, для скорости:

${\ displaystyle {\ boldsymbol {v}} = {\ frac {d} {dt}} {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ { k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d} q_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}}}$

${\ displaystyle = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {j = 1} ^ {d } q_ {j} \ {\ dot {\ boldsymbol {e_ {j}}}},}$

${\ displaystyle = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d } \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} q_ {j} \ {\ Gamma ^ {k}} _ {ij} {\ boldsymbol {e_ {k} }} {\ dot {q}} _ {i} \}$

${\ displaystyle = \ sum _ {k = 1} ^ {d} \ left ({\ dot {q}} _ {k} \ + \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} q_ {j} \ {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \,}$

с Γ-обозначением символов Кристоффеля вместо фигурных скобок. Используя тот же подход, ускорение затем

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d} {dt}} {\ boldsymbol {v}} = \ sum _ {k = 1} ^ {d} {\ dot {v}} _ { k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d} v_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}} \.}$

${\ displaystyle = \ sum _ {k = 1} ^ {d} \ left ({\ dot {v}} _ {k} \ + \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \.}$

Рассматривая соотношение для ускорения, первое суммирование содержит производные скорости по времени, которые были бы связаны с ускорением, если бы это были декартовы координаты, а второе суммирование (с символами Кристоффеля) содержит члены, связанные с тем, как изменяются единичные векторы. с течением времени.

«Состояние движения» против «координированных» фиктивных сил

Ранее в этой статье было введено различие между двумя терминологиями: фиктивные силы, которые исчезают в инерциальной системе отсчета, называются в этой статье фиктивными силами "состояния движения", а те, которые возникают в результате дифференциации в конкретной системе координат, называются называется «согласованными» фиктивными силами. Используя приведенное выше выражение для ускорения, закон движения Ньютона в инерциальной системе отсчета принимает следующий вид:

${\ displaystyle {\ boldsymbol {F}} = m {\ boldsymbol {a}} = m \ sum _ {k = 1} ^ {d} \ left ({\ dot {v}} _ {k} \ + \ сумма _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \,}$

где F - чистая реальная сила, действующая на частицу. Никаких фиктивных сил «состояния движения» нет, потому что рама инерциальна, а фиктивные силы «состояния движения» по определению равны нулю в инерциальной системе отсчета.

«Координатный» подход к закону Ньютона, приведенному выше, заключается в том, чтобы сохранить производные второго порядка от координат { q _k } по времени в качестве единственных членов в правой части этого уравнения, мотивируя это больше математическим удобством, чем физикой. С этой целью силовой закон можно переписать, взяв второе суммирование силовой части уравнения как:

${\ displaystyle {\ boldsymbol {F}} - m \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ { ij} {\ dot {q}} _ {i} {\ boldsymbol {e_ {k}}} = m {\ tilde {\ boldsymbol {a}}} \,}$

с условием, что "ускорение" теперь: ${\ displaystyle {\ tilde {\ boldsymbol {a}}}}$

${\ displaystyle {\ tilde {\ boldsymbol {a}}} = \ sum _ {k = 1} ^ {d} {\ dot {v}} _ {k} {\ boldsymbol {e_ {k}}} \. }$

В приведенном выше выражении суммирование, добавленное к силовой стороне уравнения, теперь обрабатывается так, как если бы добавленные «силы» присутствовали. Эти элементы суммирования обычно называются фиктивными силами в рамках этого «координатного» подхода, хотя в этой инерциальной системе отсчета все фиктивные силы «состояния движения» тождественно равны нулю. Более того, эти «силы» не трансформируются при преобразованиях координат как векторы . Таким образом, обозначение терминов суммирования как «фиктивные силы» использует эту терминологию для вкладов, которые полностью отличаются от любой реальной силы и от фиктивных сил «состояния движения». Эта путаница усугубляется тем, что эти «координированные» фиктивные силы разделены на две группы и имеют те же названия, что и фиктивные силы «состояния движения», то есть они разделены на «центробежные» и «кориолисовы» термины. , несмотря на то, что в них включены термины, которые не являются термином «центробежный режим движения» и термином Кориолиса. Например, эти «координатные» центробежные члены и члены Кориолиса могут быть отличными от нуля даже в инерциальной системе отсчета, где центробежная сила «состояния движения» (предмет данной статьи) и сила Кориолиса всегда равны нулю.

Если рамка не инерционная, например, во вращающейся системе отсчета, фиктивные силы «состояния движения» включаются в вышеуказанное выражение фиктивной силы «координаты». Кроме того, если «ускорение», выраженное в терминах производных скорости первого порядка по времени, приводит к выражениям, которые не являются просто производными второго порядка координат { q _k } по времени, то эти члены не являются второстепенными. порядок также вносится в силовую сторону уравнения и включается в фиктивные силы. С точки зрения лагранжевой формулировки их можно назвать обобщенными фиктивными силами. См., Например, Хильдебранда.

Формулировка динамики в терминах символов Кристоффеля и «координатной» версии фиктивных сил часто используется при проектировании роботов в связи с лагранжевой формулировкой уравнений движения.

Примечания и ссылки

дальнейшее чтение

• Описание Ньютона в Principia
• Центробежная сила реакции - электронная энциклопедия Колумбии
• М. Алонсо и Э. Дж. Финн, Фундаментальная университетская физика , Аддисон-Уэсли
• Центростремительная сила против центробежной силы - из онлайн-учебника по физике на экзамене Regents Exam от школьного округа Освего
• Центробежная сила действует внутрь около черной дыры
• Центробежная сила на сайте концепций HyperPhysics
• Список интересных ссылок
• Кеннет Франклин Райли; Майкл Пол Хобсон; Стивен Джон Бенс (2002). «Производные от базисных векторов и символов Кристоффеля» . Математические методы для физики и техники: Подробное руководство (2-е изд.). Издательство Кембриджского университета. стр. 814 и далее . ISBN 0-521-89067-5.

внешние ссылки

• Движение по плоской поверхности Java Physlet Брайана Фидлера (из Школы метеорологии Университета Оклахомы), иллюстрирующее фиктивные силы. Физлет показывает перспективу как с вращающейся, так и с невращающейся точки зрения.
• Движение над параболической поверхностью Java Physlet Брайана Фидлера (из школы метеорологии Университета Оклахомы), иллюстрирующее фиктивные силы. Физлет показывает перспективу как с вращающейся, так и с невращающейся точки зрения.
• Анимационный клип, показывающий сцены с точки зрения как инерциальной, так и вращающейся системы координат, визуализирующий Кориолисовы и центробежные силы.
• Центростремительные и центробежные силы на MathPages
• Центробежная сила при h2g2
• Джон Баэз: Центробежная сила удерживает Луну?

Смотрите также