Линия Симсона LN (красная) треугольника ABC относительно точки P на описанной окружности

В геометрии , если дан треугольник ABC и точка P на его описанной окружности , три точки, ближайшие к P на прямых AB , AC и BC, лежат на одной прямой . Линия , проходящая через эти точки является Симсон линия из P , названный в честь Роберта Симсон . Однако эта концепция была впервые опубликована Уильямом Уоллесом в 1799 году.

Обратное также верно; если три точки, ближайшие к P на трех прямых, лежат на одной прямой, и никакие две прямые не параллельны, то точка P лежит на описанной окружности треугольника, образованного этими тремя прямыми. Или, другими словами, то Симсон линия треугольника ABC и точка P является только педаль треугольник из ABC и P , который выродился в прямую линию , и это условие ограничивает геометрическое из P проследить окружность треугольника ABC .

Уравнение

Поместив треугольник в комплексную плоскость, пусть треугольник ABC с единичной описанной окружностью имеет вершины, местоположения которых имеют комплексные координаты a , b , c , и пусть P с комплексными координатами p будет точкой на описанной окружности. Линия Симсона - это множество точек z, удовлетворяющих

${\ displaystyle 2abc {\ bar {z}} - 2pz + p ^ {2} + (a + b + c) p- (bc + ca + ab) - {\ frac {abc} {p}} = 0, }$

где черта сверху означает комплексное сопряжение .

Характеристики

Линии Симсона (красные) касаются дельтовидной мышцы Штейнера (синего цвета).

• Линия Симсона вершины треугольника - это высота треугольника, опущенная из этой вершины, а линия Симсона точки, диаметрально противоположной вершине, - это сторона треугольника, противоположная этой вершине.
• Если P и Q являются точками на описанной окружности, то угол между линиями Симсона P и Q составляет половину угла дуги PQ . В частности, если точки диаметрально противоположны, их линии Симсона перпендикулярны, и в этом случае пересечение линий лежит на окружности из девяти точек.
• Полагая Н обозначим ортоцентр треугольника АВС , то Симсон линия Р делит пополам отрезок PH в точке , которая лежит на девяти точек окружности.
• Принимая во внимание два треугольника с одной и той же окружности, угол между линиями SIMSON от точки Р на окружности для обоих треугольников не зависит от Р .
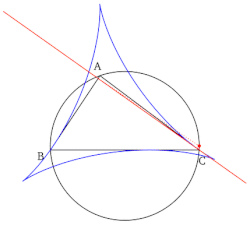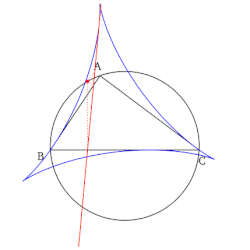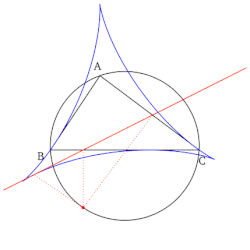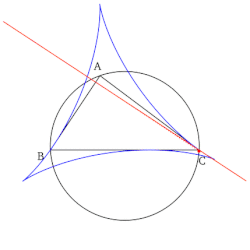
• Набор всех линий Симсона при рисовании образует конверт в форме дельтовидной мышцы, известной как дельтовид Штейнера контрольного треугольника.
• Построение линии Симсона, которая совпадает со стороной контрольного треугольника (см. Первое свойство выше), дает нетривиальную точку на этой боковой линии. Эта точка является отражением подножия высоты (сброшенной на боковую линию) относительно середины строящейся боковой линии. Кроме того, эта точка является точкой касания между стороной контрольного треугольника и его дельтовидом Штейнера.
• Четырехугольник, который не является параллелограммом, имеет одну и только одну педальную точку, называемую точкой Симсона, относительно которой ступни на четырехугольнике коллинеарны. Точка Симсона трапеции - это точка пересечения двух непараллельных сторон.
• Никакой выпуклый многоугольник с 5-ю сторонами не имеет линии Симсона.

Доказательство существования

Метод доказательства - показать это . вписанный четырехугольник, так что . является вписанным четырехугольником ( теорема Фалеса ), поэтому . Отсюда . Сейчас циклично, так что . Следовательно . ${\ displaystyle \ angle NMP + \ angle PML = 180 ^ {\ circ}}$${\ displaystyle PCAB}$${\ displaystyle \ angle PBA + \ angle ACP = \ angle PBN + \ angle ACP = 180 ^ {\ circ}}$${\ displaystyle PMNB}$${\ Displaystyle \ угол PBN + \ угол NMP = 180 ^ {\ circ}}$${\ displaystyle \ angle NMP = \ angle ACP}$${\ displaystyle PLCM}$${\ displaystyle \ angle PML = \ angle PCL = 180 ^ {\ circ} - \ angle ACP}$${\ displaystyle \ angle NMP + \ angle PML = \ angle ACP + (180 ^ {\ circ} - \ angle ACP) = 180 ^ {\ circ}}$

Альтернативное доказательство

зеленая линия - линия Симсона, синяя - перпендикуляры.

Какой бы ни была точка Z на соседнем рисунке, a + c равно 90. Кроме того, независимо от точки Z, c и b будут равны. Следовательно, мы имеем следующее:

а + с = 90

∴ a + b = 90… (c и b равны) (1)

Теперь рассмотрим величину угла: a + 90 + b.

Если мы покажем, что этот угол равен 180, то теорема Симсона доказана.

Из (1) имеем a + 90 + b = 180

QED

Обобщения

Обобщение 1

Проекции Ap, Bp, Cp на BC, CA, AB являются тремя коллинеарными точками

• Пусть ABC - треугольник, прямая ℓ проходит через центр описанной окружности O , а точка P лежит на описанной окружности. Пусть AP, BP, CP пересекаются с ℓ в точках A _p , B _p , C _p соответственно. Пусть A ₀ , B ₀ , C ₀ - проекции A _p , B _p , C _p на BC, CA, AB соответственно. Тогда A ₀ , B ₀ , C ₀ коллинеарны. Более того, новая линия проходит через середину PH , где H - ортоцентр Δ ABC . Если ℓ проходит через P , линия совпадает с линией Симсона.

Проективная версия линии Симсона

Обобщение 2

• Пусть вершины треугольника ABC лежат на конике Γ, а Q, P - две точки на плоскости. Пусть PA, PB, PC пересекают конику в точках A ₁ , B ₁ , C ₁ соответственно. QA ₁ пересекает BC в A ₂ , QB ₁ пересекает AC в B ₂ , а QC ₁ пересекает AB в C ₂ . Тогда четыре точки A ₂ , B ₂ , C ₂ и P коллинеарны, если только Q лежит на конике Γ.

Обобщение 3

• Р.Ф. Цистер обобщил теорему на циклические четырехугольники в линиях Симсона циклического четырехугольника.

Смотрите также

• Педальный треугольник
• Роберт Симсон

использованная литература

внешние ссылки

• Simson Line на сайте Cut the Knot .org
• Ф. М. Джексон и Вайстейн, Эрик В. "Линия Симсона" . MathWorld .
• Обобщение теоремы Нойберга и линии Симсона-Уоллеса в Dynamic Geometry Sketches , интерактивном эскизе динамической геометрии.