1 + 2 + 3 + 4 + ⋯ - 1 + 2 + 3 + 4 + ⋯

Первые четыре частичные суммы ряда 1 + 2 + 3 + 4 + ⋯ . Параболами являются их сглаженной асимптотой ; его отрезок по оси y равен -1/12.

Бесконечный ряд, членами которого являются натуральные числа 1 + 2 + 3 + 4 +, является расходящимся рядом . П - я частичной суммы ряда является треугольным числом

${\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}},}$

который неограниченно возрастает при стремлении n к бесконечности . Поскольку последовательность частичных сумм не может сходиться к конечному пределу , у ряда нет суммы.

Хотя на первый взгляд кажется, что ряды вообще не имеют какой-либо значимой ценности, ими можно манипулировать, чтобы получить ряд математически интересных результатов. Например, многие методы суммирования используются в математике для присвоения числовых значений даже расходящимся рядам. В частности, методы регуляризации дзета-функции и суммирования Рамануджана присваивают ряду значение -1/12, которое выражается известной формулой

${\ displaystyle 1 + 2 + 3 + 4 + \ cdots = - {\ frac {1} {12}},}$

где левая часть должна интерпретироваться как значение, полученное с помощью одного из вышеупомянутых методов суммирования, а не как сумма бесконечного ряда в ее обычном значении. Эти методы находят применение в других областях , таких как комплексный анализ , квантовой теории поля и теории струн .

В монографии по теории самогона Терри Гэннон называет это уравнение «одной из самых замечательных формул в науке».

Частичные суммы

Первые шесть треугольных чисел

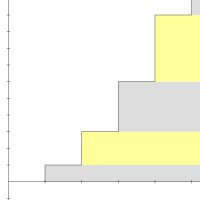
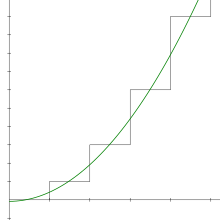
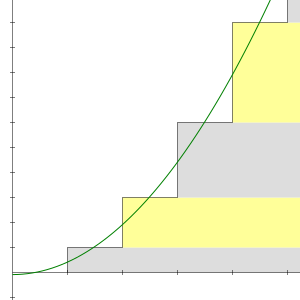
Частичные суммы ряда 1 + 2 + 3 + 4 + 5 + 6 + равны 1, 3, 6, 10, 15 и т. Д. N- я частичная сумма дается простой формулой:

${\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}}.}$

Это уравнение было известно пифагорейцам еще в шестом веке до нашей эры. Числа такой формы называются треугольными числами , потому что их можно расположить в виде равностороннего треугольника.

Бесконечная последовательность треугольных чисел расходится до + ∞, поэтому по определению бесконечный ряд 1 + 2 + 3 + 4 + ⋯ также расходится до + ∞. Расхождение является простым следствием формы ряда: члены не приближаются к нулю, поэтому ряд расходится по критерию проверки .

Суммируемость

Среди классических расходящихся рядов 1 + 2 + 3 + 4 + относительно сложно преобразовать в конечное значение. Многие методы суммирования используются для присвоения числовых значений расходящимся рядам, некоторые из которых более эффективны, чем другие. Например, суммирование Чезаро - это хорошо известный метод, который суммирует ряд Гранди , слегка расходящийся ряд 1 - 1 + 1 - 1 + , чтобы получить1/2. Суммирование Абеля - более мощный метод, который не только суммирует ряд Гранди к1/2, но также суммирует более сложный ряд 1 - 2 + 3 - 4 + ⋯ до1/4.

В отличие от приведенного выше ряда, 1 + 2 + 3 + 4 + ⋯ не суммируем по Чезаро и не суммируем по Абелю. Эти методы работают с осциллирующими расходящимися рядами, но они не могут дать конечный ответ для ряда, расходящегося до + ∞. Большинство наиболее элементарных определений суммы расходящегося ряда являются стабильными и линейными, и любой метод, который является одновременно стабильным и линейным, не может суммировать 1 + 2 + 3 + до конечного значения; см. ниже. Требуются более продвинутые методы, такие как регуляризация дзета-функции или суммирование Рамануджана . Также можно привести доводы в пользу ценности -+1/12 используя некоторые грубые эвристики, связанные с этими методами.

Эвристика

Отрывок из первой записной книжки Рамануджана, описывающий «константу» серии.

Шриниваса Рамануджан представил два вывода от « 1 + 2 + 3 + 4 + ⋯ = -+1/12"в главе 8 его первой записной книжки. Более простой и менее строгий вывод происходит в два этапа, а именно:

Первый ключевой вывод состоит в том, что ряд положительных чисел 1 + 2 + 3 + 4 + ⋯ очень похож на чередующийся ряд 1 - 2 + 3 - 4 + ⋯ . Последняя серия тоже расходится, но работать с ней намного проще; есть несколько классических методов, которые определяют его ценность, которые исследуются с 18 века.

Чтобы преобразовать ряд 1 + 2 + 3 + 4 + в 1 - 2 + 3 - 4 + ⋯ , можно вычесть 4 из второго члена, 8 из четвертого члена, 12 из шестого члена и т. Д. . Общая сумма, которую нужно вычесть, составляет 4 + 8 + 12 + 16 + ⋯ , что в 4 раза превышает исходную серию. Эти отношения можно выразить с помощью алгебры. Какой бы ни была «сумма» ряда, назовите ее c = 1 + 2 + 3 + 4 + ⋯. Затем умножьте это уравнение на 4 и вычтите второе уравнение из первого:

${\ displaystyle {\ begin {alignat} {7} c = {} && 1 + 2 && {} + 3 + 4 && {} + 5 + 6 + \ cdots \\ 4c = {} && 4 && {} + 8 && {} + 12+ \ cdots \\ c-4c = {} && 1-2 && {} + 3-4 && {} + 5-6 + \ cdots \ end {alignat}}}$

Второе ключевое открытие заключается в том, что чередующийся ряд 1-2 + 3-4 + ⋯ является разложением в формальный степенной ряд функции1/(1 + х ) ²но с x, определенным как 1. Соответственно, Рамануджан пишет

${\ displaystyle -3c = 1-2 + 3-4 + \ cdots = {\ frac {1} {(1 + 1) ^ {2}}} = {\ frac {1} {4}}.}$

Разделив обе части на −3, получим c  =  -+1/12.

Вообще говоря, неправильно манипулировать бесконечными рядами, как если бы они были конечными суммами. Например, если нули вставляются в произвольные позиции расходящегося ряда, можно получить результаты, которые не являются самосогласованными, не говоря уже о совместимости с другими методами. В частности, шаг 4 c = 0 + 4 + 0 + 8 + ⋯ не оправдывается одним только аддитивным законом тождества . В крайнем случае добавление одного нуля в начало ряда может привести к другому результату.

Один из способов исправить эту ситуацию и ограничить места, где могут быть вставлены нули, - это отслеживать каждый член в ряду, добавляя зависимость от некоторой функции. В ряду 1 + 2 + 3 + 4 + ⋯ каждый член n - это просто число. Если термин n преобразован в функцию n - ^s , где s - комплексная переменная, то можно гарантировать, что добавляются только одинаковые термины. Результирующим рядом можно управлять более строго, а переменная s может быть установлена ​​в -1 позже. Реализация этой стратегии называется регуляризацией дзета-функции .

Регуляризация дзета-функции

График ζ ( s ). При s > 1 ряд сходится и ζ ( s )> 1 . Аналитическое продолжение вокруг полюса при s = 1 приводит к области отрицательных значений, включая ζ (−1) = -+1/12.

При регуляризации дзета-функции ряд заменяется рядом . Последняя серия является примером серии Дирихле . Когда действительная часть s больше 1, ряд Дирихле сходится, а его сумма является дзета-функцией Римана ζ ( s ). С другой стороны, ряд Дирихле расходится, когда действительная часть s меньше или равна 1, поэтому, в частности, ряд 1 + 2 + 3 + 4 + ⋯ , полученный при установке s = –1, не сходится . Преимущество введения дзета-функции Римана состоит в том, что ее можно определить для других значений s путем аналитического продолжения . Тогда можно определить дзета-регуляризованную сумму 1 + 2 + 3 + 4 + ⋯ как ζ (−1). ${\ textstyle \ сумма _ {п = 1} ^ {\ infty} п}$${\ textstyle \ sum _ {п = 1} ^ {\ infty} п ^ {- s}}$

С этого момента есть несколько способов доказать, что ζ (−1) = -+1/12. Один метод, аналогичный рассуждениям Эйлера, использует взаимосвязь между дзета-функцией Римана и эта-функцией Дирихле η ( s ). Эта функция определяется чередующимся рядом Дирихле, поэтому этот метод аналогичен более ранним эвристикам. Когда оба ряда Дирихле сходятся, один имеет тождества:

${\ displaystyle {\ begin {alignat} {7} \ zeta (s) & {} = {} & 1 ^ {- s} +2 ^ {- s} && {} + 3 ^ {- s} + 4 ^ { -s} && {} + 5 ^ {- s} +6 ^ {- s} + \ cdots & \\ 2 \ times 2 ^ {- s} \ zeta (s) & {} = {} & 2 \ times 2 ^ {- s} && {} + 2 \ times 4 ^ {- s} && {} + 2 \ times 6 ^ {- s} + \ cdots & \\\ left (1-2 ^ {1-s} \ вправо) \ zeta (s) & {} = {} & 1 ^ {- s} -2 ^ {- s} && {} + 3 ^ {- s} -4 ^ {- s} && {} + 5 ^ { -s} -6 ^ {- s} + \ cdots & = \ eta (s). \ end {alignat}}}$

Тождество остается в силе, когда обе функции расширяются путем аналитического продолжения, чтобы включить значения s, для которых указанные выше ряды расходятся. Подставляя s = −1 , получаем −3 ζ (−1) = η (−1). Теперь вычисление η (−1) - более простая задача, поскольку эта функция равна сумме Абеля ее определяющего ряда, что является односторонним пределом : ${\ Displaystyle (1-2 ^ {1-s}) \ zeta (s) = \ eta (s)}$

${\ displaystyle -3 \ zeta (-1) = \ eta (-1) = \ lim _ {x \ to 1 ^ {-}} \ left (1-2x + 3x ^ {2} -4x ^ {3} + \ cdots \ right) = \ lim _ {x \ to 1 ^ {-}} {\ frac {1} {(1 + x) ^ {2}}} = {\ frac {1} {4}}. }$

Разделив обе части на −3, получим ζ (−1) = -+1/12.

Обрезка регуляризации

Ряд 1 + 2 + 3 + 4 + ⋯

После сглаживания

Асимптотика сглаживания. У -intercept параболы -+1/12.

Метод регуляризации с использованием функции отсечения может «сгладить» ряд, чтобы прийти к -+1/12. Сглаживание - это концептуальный мост между регуляризацией дзета-функции с его опорой на комплексный анализ и суммированием Рамануджана с его сокращением до формулы Эйлера – Маклорена . Вместо этого метод работает непосредственно с консервативными преобразованиями ряда, используя методы реального анализа .

Идея состоит в том, чтобы заменить некорректную дискретную серию сглаженной версией. ${\ displaystyle \ textstyle \ sum _ {n = 0} ^ {N} n}$

${\ displaystyle \ sum _ {n = 0} ^ {\ infty} nf \ left ({\ frac {n} {N}} \ right),}$

где f - срезающая функция с соответствующими свойствами. Функция отсечения должна быть нормирована на f (0) = 1 ; эта нормализация отличается от той, которая используется в дифференциальных уравнениях. Функция отсечения должна иметь достаточно ограниченных производных, чтобы сгладить складки в ряду, и должна уменьшаться до 0 быстрее, чем ряд растет. Для удобства можно потребовать, чтобы f была гладкой , ограниченной и с компактным носителем . Затем можно доказать, что эта сглаженная сумма асимптотична по отношению к -+1/12+ CN ² , где C - постоянная, зависящая от f . Постоянный член асимптотического разложения не зависит от f : это обязательно то же самое значение, которое дает аналитическое продолжение,  -+1/12.

Рамануджан суммирование

Рамануйян сумма из 1 + 2 + 3 + 4 + ⋯ также  -+1/12. Рамануджан написал в своем втором письме Г. Х. Харди от 27 февраля 1913 г .:

«Дорогой сэр, я очень удовлетворен на просматривал Ваше письмо от 8 февраля 1913 года я ожидал от Вас ответа , подобную той , которую профессор математики в Лондоне написал просит меня изучать тщательно Бромвич «s Infinite Series и не падать в ловушки расходящихся рядов ... Я сказал ему, что сумма бесконечного числа членов ряда: 1 + 2 + 3 + 4 + ⋯ = -+1/12по моей теории. Если я скажу вам это, вы сразу же укажете мне сумасшедший дом как мою цель. Я расширяю это просто, чтобы убедить вас, что вы не сможете следовать моим методам доказательства, если я в одном письме укажу те строки, по которым я исхожу. … »

Суммирование Рамануджана - это метод выделения постоянного члена в формуле Эйлера – Маклорена для частичных сумм ряда. Для функции f классическая сумма Рамануджана ряда определяется как ${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {\ infty} f (k)}$

${\ displaystyle c = - {\ frac {1} {2}} f (0) - \ sum _ {k = 1} ^ {\ infty} {\ frac {B_ {2k}} {(2k)!}} е ^ {(2k-1)} (0),}$

где f ^{(2 k −1)} - (2 k  - 1) -я производная от f, а B _{2 k} - 2 k -ое число Бернулли : B ₂ =1/6, B ₄ = -+1/30, и так далее. Положив f ( x ) = x , первая производная f равна 1, а все остальные члены равны нулю, поэтому

${\ displaystyle c = - {\ frac {1} {6}} \ times {\ frac {1} {2!}} = - {\ frac {1} {12}}.}$

Чтобы избежать противоречий, современная теория суммирования Рамануджана требует, чтобы f была "регулярной" в том смысле, что производные f более высокого порядка затухают достаточно быстро, чтобы остаточные члены в формуле Эйлера-Маклорена стремились к 0. Рамануджан молчаливо предполагал это. имущество. Требование регулярности предотвращает использование суммирования Рамануджана для разнесенных рядов, таких как 0 + 2 + 0 + 4 + , потому что ни одна обычная функция не принимает эти значения. Вместо этого такой ряд должен интерпретироваться с помощью регуляризации дзета-функции. По этой причине Харди рекомендует «с большой осторожностью» применять суммы Рамануджана известных рядов, чтобы найти суммы связанных рядов.

Несостоятельность устойчивых линейных методов суммирования

Линейный и устойчивый метод суммирования не может суммировать ряды 1 + 2 + 3 + ⋯ до любого конечного значения. (Стабильный означает, что добавление члена в начало ряда увеличивает сумму на ту же величину.) Это можно увидеть следующим образом. Если

1 + 2 + 3 + ⋯ = х

затем добавление 0 к обеим сторонам дает

0 + 1 + 2 + ⋯ = 0 + х = х

по стабильности. По линейности можно вычесть второе уравнение из первого (вычитая каждый компонент второй строки из первой строки в столбцах), чтобы получить

1 + 1 + 1 + ⋯ = х - х = 0.

Добавление 0 к обеим сторонам снова дает

0 + 1 + 1 + 1 + ⋯ = 0,

и вычитание двух последних серий дает

1 + 0 + 0 + ⋯ = 0,

противоречащая стабильности.

Следовательно, любой метод, который дает конечное значение сумме 1 + 2 + 3 +, не является устойчивым или нелинейным.

Физика

В теории бозонных струн делается попытка вычислить возможные уровни энергии струны, в частности, самый низкий уровень энергии. Говоря неформально, каждую гармонику струны можно рассматривать как набор D  - 2 независимых квантовых гармонических осцилляторов , по одному для каждого поперечного направления , где D - размерность пространства-времени. Если основная частота колебаний равна ω , то энергия в осцилляторе, вносящая вклад в n-ю гармонику, равна nħω / 2. Таким образом, используя расходящийся ряд, сумма по всем гармоникам равна - ħω ( D - 2) / 24 . В конечном итоге именно этот факт в сочетании с теоремой Годдарда – Торна приводит к тому, что теория бозонных струн не может быть последовательной в измерениях, отличных от 26.

Регуляризация 1 + 2 + 3 + 4 + также участвует в вычислении силы Казимира для скалярного поля в одномерном измерении. Для сглаживания ряда достаточно экспоненциальной функции отсечки, что свидетельствует о том, что моды произвольно высоких энергий не блокируются проводящими пластинами. Пространственная симметрия задачи отвечает за сокращение квадратичного члена разложения. Остается только постоянный член -1/12, и отрицательный знак этого результата отражает тот факт, что сила Казимира притягивает.

Аналогичные вычисления используются в трех измерениях с использованием дзета-функции Эпштейна вместо дзета-функции Римана.

История

Неясно, подвел ли Леонард Эйлер серию к -+1/12. Согласно Моррису Клайну , ранние работы Эйлера по расходящимся рядам основывались на функциональных разложениях, из которых он заключил 1 + 2 + 3 + 4 + ⋯ = ∞ . Согласно Раймонду Аюбу, тот факт, что расходящийся дзета-ряд не суммируется по Абелю, не позволил Эйлеру использовать дзета-функцию так же свободно, как и эту-функцию, и он «не мог придать значение» этой серии. Другие авторы приписывают эту сумму Эйлеру, предполагая, что Эйлер расширил бы связь между дзета- и эта-функциями до отрицательных целых чисел. В первичной литературе ряд 1 + 2 + 3 + 4 + упоминается в публикации Эйлера 1760 года De seriebus divergentibus вместе с расходящимся геометрическим рядом 1 + 2 + 4 + 8 + . Эйлер намекает, что ряды этого типа имеют конечные отрицательные суммы, и объясняет, что это означает для геометрических рядов, но не возвращается к обсуждению 1 + 2 + 3 + 4 + ⋯ . В той же публикации Эйлер пишет, что сумма 1 + 1 + 1 + 1 + бесконечна.

В популярных СМИ

Роман Дэвида Ливитта « Индийский служащий» 2007 года включает сцену, в которой Харди и Литтлвуд обсуждают значение этой серии. Они заключают, что Рамануджан заново открыл ζ (−1), и принимают строчку «сумасшедшее убежище» во втором письме как знак того, что Рамануджан играет с ними.

В пьесе Саймона МакБёрни « Исчезающее число» 2007 года основное внимание уделяется сериалу в начальной сцене. Главная героиня, Рут, входит в лекционный зал и представляет идею расходящейся серии перед тем, как провозгласить: «Я собираюсь показать вам кое-что действительно захватывающее», а именно 1 + 2 + 3 + 4 + ⋯ = -+1/12. Когда Рут приступает к выводу функционального уравнения дзета-функции, другой актер обращается к аудитории, признавая, что они актеры: «Но математика реальна. Это ужасно, но реально».

В январе 2014 года Numberphile выпустила на YouTube видео по сериалу, которое за первый месяц собрало более 1,5 миллиона просмотров. 8-минутное видео ведет Тони Падилла, физик из Ноттингемского университета . Падилья начинает с 1 - 1 + 1 - 1 + ⋯ и 1 - 2 + 3 - 4 + ⋯ и связывает последнее с 1 + 2 + 3 + 4 + ⋯, используя посрочное вычитание, подобное аргументу Рамануджана. Numberphile также выпустила 21-минутную версию видео с участием физика из Ноттингема Эда Коупленда , который более подробно описывает, как 1 - 2 + 3 - 4 + ⋯ =1/4в виде суммы Абеля и 1 + 2 + 3 + 4 + ⋯ = -+1/12как ζ (−1). Получив жалобы на отсутствие строгости в первом видео, Падилья также написал на своей веб-странице объяснение, связанное с манипуляциями в видео с идентичностями между аналитическими продолжениями соответствующей серии Дирихле.

В репортаже The New York Times о видео Numberphile математик Эдвард Френкель прокомментировал: «Этот расчет - один из наиболее охраняемых секретов математики. Никто со стороны об этом не знает».

Освещение этой темы в журнале Smithsonian описывает видео Numberphile как вводящее в заблуждение и отмечает, что интерпретация суммы как -+1/12опирается на специальное значение знака равенства из методов аналитического продолжения , в которых равное означает, что связано с .

использованная литература

Библиография

дальнейшее чтение

внешние ссылки

• Лэмб Э. (2014), « Действительно ли 1 + 2 + 3… Равно –1/12? », Scientific American Blogs.
• Результаты этой недели по математической физике (неделя 124) , (неделя 126) , (неделя 147) , (неделя 213)
  • Доказательство Эйлера, что 1 + 2 + 3 + ⋯ = −1/12 - от Джона Баэза
  • Джон Баэз (19 сентября 2008 г.). «Любимые числа: 24» (PDF) .
• Формула Эйлера-Маклорена, числа Бернулли, дзета - функция, и в режиме реального переменная аналитическое продолжение по Теренс Тао
• Рекурсивная оценка дзеты отрицательных целых чисел от Лубоса Мотл
• Ссылка на видео Numberphile 1 + 2 + 3 + 4 + 5 + ... = –1/12
  • Сумма натуральных чисел (второе доказательство и дополнительные кадры) включает демонстрацию метода Эйлера.
  • Что мы получим, если сложим все натуральные числа? ответ на комментарии к видео Тони Падиллы
  • Статья по теме из New York Times
  • Почему –1/12 - это золотой самородок , продолжающий видео Numberphile с Эдвардом Френкелем
• Дивергентная серия: почему 1 + 2 + 3 + ⋯ = −1/12, автор Брайдон Кейс из Университета Аризоны