Нормальная форма Хомского - Chomsky normal form

В формальном языке теории, контекстно-свободная грамматика , G , называется в нормальной форме Хомского (первый описываемого Хомского ) , если все его правила производства имеют вид:

A → BC , или

A → a , или

S → ε,

где A , B и C - нетерминальные символы , буква a - конечный символ (символ, представляющий постоянное значение), S - начальный символ, а ε обозначает пустую строку . Кроме того , ни В , ни С может быть начальным символом , а третье правило производство может появиться только тогда , когда ε в L ( G ), язык производства контекстно-свободной грамматики G .

Каждая грамматика в нормальной форме Хомского является контекстно-независимой , и, наоборот, каждая контекстно-свободная грамматика может быть преобразована в эквивалентную грамматику в нормальной форме Хомского, размер которой не превышает квадрата размера исходной грамматики.

Преобразование грамматики в нормальную форму Хомского

Чтобы преобразовать грамматику в нормальную форму Хомского, применяется последовательность простых преобразований в определенном порядке; это описано в большинстве учебников по теории автоматов. Представленная здесь презентация следует за Hopcroft, Ullman (1979), но адаптирована для использования имен преобразований из Lange, Leiß (2009). Каждое из следующих преобразований устанавливает одно из свойств, необходимых для нормальной формы Хомского.

СТАРТ: удалите начальный символ с правой стороны.

Введите новый начальный символ S ₀ и новое правило

S ₀ → S ,

где S - предыдущий начальный символ. Это не меняет язык, созданный грамматикой, и S ₀ не встречается в правой части любого правила.

СРОК: Отменить правила с неуединенными терминалами

Чтобы устранить каждое правило

А → Х ₁ ... а ... Х _n

с терминальным символом a, который не является единственным символом в правой части, введите для каждого такого терминала новый нетерминальный символ N _a и новое правило

N _a → a .

Измените каждое правило

А → Х ₁ ... а ... Х _n

к

A → X ₁ ... N _a ... X _n .

Если в правой части встречается несколько оконечных символов, одновременно замените каждый из них соответствующим нетерминальным символом. Это не меняет язык, созданный грамматикой.

BIN: исключите правые части с более чем 2 нетерминалами

Заменить каждое правило

А → Х ₁ Х ₂ ... Х _n

с более чем 2 нетерминалами X ₁ , ..., X _n по правилам

А → Х ₁ А ₁ ,

А ₁ → Х ₂ А ₂ ,

...,

A _{n -2} → X _{n -1} X _n ,

где A _i - новые нетерминальные символы. Опять же, это не меняет язык, созданный грамматикой.

DEL: отменить ε-правила

Ε-правило - это правило вида

A → ε,

где A не S ₀ , начальный символ грамматики.

Чтобы исключить все правила этой формы, сначала определите набор всех нетерминалов, которые производят ε. Хопкрофт и Ульман (1979) называют такие нетерминалы обнуляемыми и вычисляют их следующим образом:

Если существует правило A → ε, то A допускает значение NULL.
Если существует правило A → X ₁ ... X _n и каждый X _i допускает значение NULL, то A также допускает значение NULL.

Получите промежуточную грамматику, заменив каждое правило

А → Х ₁ ... Х _n

во всех версиях с пропущенным X _i, допускающим значение NULL . Путем удаления из этой грамматики каждого ε-правила, если его левая часть не является начальным символом, получается преобразованная грамматика.

Например, в следующей грамматике с начальным символом S ₀ ,

S ₀ → AbB | C

B → AA | AC

C → b | c

A → a | ε

нетерминал A , а следовательно, и B , не допускает значения NULL, в то время как ни C, ни S ₀ не допускаются . Таким образом получается следующая промежуточная грамматика:

S ₀ → A b B | A b B | A b B | A b B | C

B → AA | A A | A A | A ε A | A C | А С

C → b | c

A → a | ε

В этой грамматике все ε-правила были « встроены в сайт вызова». На следующем шаге их можно удалить, получив грамматику:

S ₀ → AbB | Ab | bB | б | C

B → AA | А | AC | C

C → b | c

А → а

Эта грамматика создает тот же язык, что и исходный пример грамматики, а именно. { ab , aba , abaa , abab , abac , abb , abc , b , bab , bac , bb , bc , c }, но не имеет ε-правил.

UNIT: исключить правила для юнитов

Единичное правило - это правило формы

А → Б ,

где A , B - нетерминальные символы. Чтобы удалить его, для каждого правила

B → X ₁ ... X _n ,

где X ₁ ... X _n - строка нетерминалов и терминалов, добавьте правило

А → Х ₁ ... Х _n

кроме случаев, когда это правило юнита уже было (или удаляется).

Порядок преобразований

Взаимное сохранение
результатов трансформации
Y Икс	НАЧАЛО	СРОК	BIN	DEL	ЕД. ИЗМ
Преобразование X всегда сохраняет ( Y) соотв. может уничтожить ( N) результат Y :
НАЧАЛО
СРОК
BIN
DEL
ЕД. ИЗМ				( Y) ^*
^*UNIT сохраняет результат DEL, если START был вызван ранее.

При выборе порядка, в котором должны применяться вышеуказанные преобразования, необходимо учитывать, что некоторые преобразования могут разрушить результат, достигнутый другими. Например, START повторно вводит правило юнита, если оно применяется после UNIT . В таблице показано, какие заказы принимаются.

Более того, наихудшее увеличение размера грамматики зависит от порядка преобразования. Использование | G | для обозначения размера исходной грамматики G размер увеличения в худшем случае может находиться в диапазоне от | G | ² к 2 ^{2 | G |}, в зависимости от используемого алгоритма преобразования. Размер увеличения грамматики зависит от порядка между DEL и BIN . Он может быть экспоненциальным, когда сначала выполняется DEL , но в противном случае - линейным. UNIT может привести к квадратичному увеличению размера грамматики. Упорядочения START , TERM , BIN , DEL , UNIT и START , BIN , DEL , UNIT , TERM приводят к наименьшему (т.е. квадратичному) разрушению.

Пример

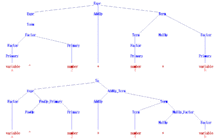
Абстрактное синтаксическое дерево из арифметического выражения « в ^ 2 + 4 * б » WRT. пример грамматики ( вверху ) и ее нормальная форма Хомского ( внизу )

Следующая грамматика с начальным символом Expr описывает упрощенную версию набора всех синтаксических допустимых арифметических выражений в таких языках программирования, как C или Algol60 . И число, и переменная здесь считаются терминальными символами для простоты, поскольку во внешнем интерфейсе компилятора их внутренняя структура обычно не рассматривается анализатором . Конечный символ «^» обозначает возведение в степень в Algol60.

Выражение	→ Срок	\| Expr AddOp Term	\| Срок действия AddOp
Срок	→ Фактор	\| Срок MulOp Factor
Фактор	→ Первичный	\| Фактор ^ Первичный
Начальный	→ номер	\| Переменная	\| ( Выражение )
AddOp	→ +	\| -
MulOp	→ *	\| /

На шаге «START» описанного выше алгоритма преобразования в грамматику добавляется только правило S ₀ → Expr . После шага «TERM» грамматика выглядит так:

S ₀	→ Выражение
Выражение	→ Срок	\| Expr AddOp Term	\| Срок действия AddOp
Срок	→ Фактор	\| Срок MulOp Factor
Фактор	→ Первичный	\| Фактор PowOp Первичный
Начальный	→ номер	\| Переменная	\| Открыть Expr Close
AddOp	→ +	\| -
MulOp	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→)

После шага «БИН» получается следующая грамматика:

S ₀	→ Выражение
Выражение	→ Срок	\| Expr AddOp_Term	\| Срок действия AddOp
Срок	→ Фактор	\| Срок MulOp_Factor
Фактор	→ Первичный	\| Фактор PowOp_Primary
Начальный	→ номер	\| Переменная	\| Открыть Expr_Close
AddOp	→ +	\| -
MulOp	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→)
AddOp_Term	→ Срок действия AddOp
MulOp_Factor	→ Фактор MulOp
PowOp_Primary	→ Первичный PowOp
Expr_Close	→ Выражение Закрыть

Поскольку ε-правил нет, шаг «DEL» не меняет грамматики. После шага «UNIT» получается следующая грамматика в нормальной форме Хомского:

S ₀	→ номер	\| Переменная	\| Открыть Expr_Close	\| Фактор PowOp_Primary	\| Срок MulOp_Factor	\| Expr AddOp_Term	\| Срок действия AddOp
Выражение	→ номер	\| Переменная	\| Открыть Expr_Close	\| Фактор PowOp_Primary	\| Срок MulOp_Factor	\| Expr AddOp_Term	\| Срок действия AddOp
Срок	→ номер	\| Переменная	\| Открыть Expr_Close	\| Фактор PowOp_Primary	\| Срок MulOp_Factor
Фактор	→ номер	\| Переменная	\| Открыть Expr_Close	\| Фактор PowOp_Primary
Начальный	→ номер	\| Переменная	\| Открыть Expr_Close
AddOp	→ +	\| -
MulOp	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→)
AddOp_Term	→ Срок действия AddOp
MulOp_Factor	→ Фактор MulOp
PowOp_Primary	→ Первичный PowOp
Expr_Close	→ Выражение Закрыть

Н введенный в шаге «СРОК» являются PowOp , Открыть и Закрыть . _Я введенный в шаге «БИН» являются AddOp_Term , MulOp_Factor , PowOp_Primary и Expr_Close .

Альтернативное определение

Приведенная форма Хомского

Другой способ определить нормальную форму Хомского:

Формальная грамматика в Хомский уменьшенный форму , если все ее правила производства имеют вид:

{\ Displaystyle A \ rightarrow \, BC}

или же

{\ Displaystyle A \ rightarrow \, а}

,

где , и - нетерминальные символы, а - конечный символ . При использовании этого определения или может быть начальным символом. Только те контекстно-свободные грамматики, которые не генерируют пустую строку, могут быть преобразованы в сокращенную форму Хомского. ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle C}$ ${\ displaystyle a}$ ${\ displaystyle B}$ ${\ displaystyle C}$

Нормальная форма Флойда

В письме, в котором он предложил термин « форма Бэкуса-Наура» (BNF), Дональд Э. Кнут подразумевал BNF, «синтаксис, в котором все определения имеют такую форму, можно сказать, в« нормальной форме Флойда »»,

{\ displaystyle \ langle A \ rangle :: = \, \ langle B \ rangle \ mid \ langle C \ rangle}

или же

{\ displaystyle \ langle A \ rangle :: = \, \ langle B \ rangle \ langle C \ rangle}

или же

{\ Displaystyle \ langle A \ rangle :: = \, а}

,

где , и - нетерминальные символы, а - конечный символ , потому что Роберт У. Флойд обнаружил, что любой синтаксис BNF может быть преобразован в указанный выше в 1961 году. Но он отказался от этого термина, «поскольку, несомненно, многие люди независимо использовали этот простой факт в их собственная работа, и дело здесь лишь в основных соображениях записки Флойда ". В то время как в записке Флойда цитируется оригинальная статья Хомского 1959 года, в письме Кнута нет. ${\ displaystyle \ langle A \ rangle}$ ${\ displaystyle \ langle B \ rangle}$ ${\ displaystyle \ langle C \ rangle}$ ${\ displaystyle a}$

Заявление

Помимо своей теоретической значимости, преобразование CNF используется в некоторых алгоритмах в качестве этапа предварительной обработки, например, в алгоритме CYK , восходящем синтаксическом анализе для контекстно-свободных грамматик и его варианте вероятностного CKY.

Смотрите также

Форма Бэкуса – Наура
CYK алгоритм
Нормальная форма Грейбаха
Курода нормальная форма
Лемма о накачке для контекстно-свободных языков - ее доказательство опирается на нормальную форму Хомского

Заметки

дальнейшее чтение

Коул, Ричард. Преобразование CFG в CNF (нормальная форма Хомского) , 17 октября 2007 г. (pdf) - использует порядок TERM, BIN, START, DEL, UNIT.
Джон Мартин (2003). Введение в языки и теорию вычислений . Макгроу Хилл. ISBN 978-0-07-232200-2. (Страницы 237–240 раздела 6.6: упрощенные и нормальные формы.)
Майкл Сипсер (1997). Введение в теорию вычислений . PWS Publishing. ISBN 978-0-534-94728-6. (Страницы 98–101 раздела 2.1: контекстно-свободные грамматики. Страница 156.)
Сипсер, Майкл. Введение в теорию вычислений, 2-е издание.
Александр Медуна (6 декабря 2012 г.). Автоматы и языки: теория и приложения . Springer Science & Business Media. ISBN 978-1-4471-0501-5.

[1] Хомский, Ноам (1959). «О некоторых формальных свойствах грамматик» . Информация и контроль . 2 (2): 137–167. DOI : 10.1016 / S0019-9958 (59) 90362-6 . Здесь: раздел 6, стр. 152 и далее.

[2] Д'Антони, Лорис. «Страница 7, Лекция 9: Алгоритмы анализа снизу вверх» (PDF) . CS536-S21 Введение в языки программирования и компиляторы . Университет Висконсин-Мэдисон.

[Hopcroft.Ullman.1979-3] ^ ^a ^b ^c ^d ^e ^f Хопкрофт, Джон Э .; Ульман, Джеффри Д. (1979). Введение в теорию автоматов, языки и вычисления . Ридинг, Массачусетс: издательство Addison-Wesley Publishing. ISBN 978-0-201-02988-8.

[5] Хопкрофт, Джон Э .; Мотвани, Раджив; Ульман, Джеффри Д. (2006). Введение в теорию автоматов, языки и вычисления (3-е изд.). Эддисон-Уэсли. ISBN 978-0-321-45536-9. Раздел 7.1.5, стр. 272

[6] Рич, Элейн (2007). Автоматы, вычислимость и сложность: теория и приложения (1-е изд.). Прентис-Холл. ISBN 978-0132288064.

[7] Вегенер, Инго (1993). Теоретическая информатика - Eine algorithmmenorientierte Einführung . Leitfäden und Mongraphien der Informatik (на немецком языке). Штутгарт: BG Teubner. ISBN 978-3-519-02123-0.Раздел 6.2 «Die Chomsky-Normalform für kontextfreie Grammatiken», с. 149–152

[Lange.Leis.2009-8] Ланге, Мартин; Лайс, Ганс (2009). «В CNF или не в CNF? Эффективная, но презентабельная версия алгоритма CYK» (PDF) . Informatica Didactica . 8 .

[13] Хопкрофт и др. (2006)

[14] Флойд, Роберт В. (1961). «Заметка о математической индукции в грамматиках фразовой структуры» (PDF) . Информация и контроль . 4 (4): 353–358. DOI : 10.1016 / S0019-9958 (61) 80052-1 . Здесь: с.354

[knuth1964-15] Кнут, Дональд Э. (декабрь 1964). «Нормальная форма Бэкуса против формы Бэкуса Наура». Коммуникации ACM . 7 (12): 735–736. DOI : 10.1145 / 355588.365140 . S2CID 47537431 .

[16] Джурафски, Даниэль; Мартин, Джеймс Х. (2008). Обработка речи и языка (2-е изд.). Пирсон Прентис Холл. п. 465. ISBN 978-0-13-187321-6.

Languages

In other projects

Нормальная форма Хомского - Chomsky normal form

СОДЕРЖАНИЕ

Преобразование грамматики в нормальную форму Хомского

СТАРТ: удалите начальный символ с правой стороны.

СРОК: Отменить правила с неуединенными терминалами

BIN: исключите правые части с более чем 2 нетерминалами

DEL: отменить ε-правила

UNIT: исключить правила для юнитов

Порядок преобразований

Пример

Альтернативное определение

Приведенная форма Хомского

Нормальная форма Флойда

Заявление

Смотрите также

Заметки

Рекомендации

дальнейшее чтение