Соответствующий фильтр - Matched filter

В обработке сигналов , А согласованный фильтр получается путем соотнесения известного задержанного сигнала , или шаблона , с неизвестным сигналом для обнаружения присутствия шаблона в неизвестном сигнале. Это эквивалентно свертке неизвестного сигнала с сопряженной версией шаблона с обращенной во времени. Согласованный фильтр - это оптимальный линейный фильтр для максимизации отношения сигнал / шум (SNR) в присутствии аддитивного стохастического шума .

Согласованные фильтры обычно используются в радарах , в которых отправляется известный сигнал, а отраженный сигнал исследуется на предмет общих элементов исходящего сигнала. Сжатие импульсов является примером согласованной фильтрации. Это так называется, потому что импульсная характеристика согласована с входными импульсными сигналами. Двумерные согласованные фильтры обычно используются при обработке изображений , например, для улучшения отношения сигнал / шум при рентгеновских наблюдениях. Согласованная фильтрация - это метод демодуляции с использованием фильтров LTI (линейный инвариантный во времени) для максимального увеличения SNR. Первоначально он был также известен как Северный фильтр .

Вывод

Вывод через матричную алгебру

В следующем разделе выводится согласованный фильтр для системы с дискретным временем . Вывод для системы с непрерывным временем аналогичен с заменой сумм интегралами.

Согласованный фильтр - это линейный фильтр, который максимизирует отношение выходного сигнала к шуму . ${\ displaystyle h}$

${\ Displaystyle \ Y [N] = \ сумма _ {к = - \ infty} ^ {\ infty} ч [nk] x [k],}$

где - вход как функция независимой переменной , а - отфильтрованный выход. Хотя мы чаще всего выражаем фильтры как импульсную характеристику систем свертки, как указано выше (см. Теорию систем LTI ), проще всего думать о согласованном фильтре в контексте внутреннего продукта , который мы вскоре увидим. ${\ Displaystyle х [к]}$${\ displaystyle k}$${\ Displaystyle у [п]}$

Мы можем получить линейный фильтр, который максимизирует отношение выходного сигнала к шуму, используя геометрический аргумент. Интуиция, лежащая в основе согласованного фильтра, основана на корреляции принятого сигнала (вектора) с фильтром (другим вектором), который параллелен сигналу, максимизируя внутренний продукт. Это усиливает сигнал. Когда мы рассматриваем аддитивный стохастический шум, мы сталкиваемся с дополнительной проблемой минимизации выхода из-за шума путем выбора фильтра, ортогонального шуму.

Определим проблему формально. Мы ищем фильтр, такой, чтобы максимизировать отношение выходного сигнала к шуму, где выходной сигнал является внутренним произведением фильтра и наблюдаемого сигнала . ${\ displaystyle h}$${\ displaystyle x}$

Наш наблюдаемый сигнал состоит из желаемого сигнала и аддитивного шума : ${\ displaystyle s}$${\ displaystyle v}$

${\ Displaystyle \ х = s + v. \,}$

Давайте определим ковариационную матрицу шума, напоминая себе, что эта матрица имеет эрмитову симметрию , свойство, которое станет полезным при выводе:

${\ Displaystyle \ R_ {v} = E \ {vv ^ {\ mathrm {H}} \} \,}$

где обозначает сопряженное транспонирование о , и обозначает ожидание . Назовем наш выход внутренним произведением нашего фильтра и наблюдаемого сигнала таким образом, что ${\ displaystyle v ^ {\ mathrm {H}}}$${\ displaystyle v}$${\ displaystyle E}$${\ displaystyle y}$

${\ displaystyle \ y = \ sum _ {k = - \ infty} ^ {\ infty} h ^ {*} [k] x [k] = h ^ {\ mathrm {H}} x = h ^ {\ mathrm {H}} s + h ^ {\ mathrm {H}} v = y_ {s} + y_ {v}.}$

Теперь мы определяем отношение сигнал / шум, которое является нашей целевой функцией, как отношение выходной мощности из-за полезного сигнала к выходной мощности из-за шума:

${\ displaystyle \ mathrm {SNR} = {\ frac {| y_ {s} | ^ {2}} {E \ {| y_ {v} | ^ {2} \}}}.}$

Перепишем вышесказанное:

${\ displaystyle \ mathrm {SNR} = {\ frac {| h ^ {\ mathrm {H}} s | ^ {2}} {E \ {| h ^ {\ mathrm {H}} v | ^ {2} \}}}.}$

Мы хотим максимизировать это количество, выбирая . Раскладывая знаменатель нашей целевой функции, мы имеем ${\ displaystyle h}$

${\ displaystyle \ E \ {| h ^ {\ mathrm {H}} v | ^ {2} \} = E \ {(h ^ {\ mathrm {H}} v) {(h ^ {\ mathrm {H) }} v)} ^ {\ mathrm {H}} \} = h ^ {\ mathrm {H}} E \ {vv ^ {\ mathrm {H}} \} h = h ^ {\ mathrm {H}} R_ {v} ч. \,}$

Теперь наш становится ${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| h ^ {\ mathrm {H}} s | ^ {2}} {h ^ {\ mathrm {H}} R_ {v} h}}.}$

Мы перепишем это выражение с некоторыми манипуляциями с матрицей. Причина этой, казалось бы, контрпродуктивной меры станет очевидной в ближайшее время. Используя эрмитову симметрию ковариационной матрицы , мы можем записать ${\ displaystyle R_ {v}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}},}$

Мы хотели бы найти верхнюю границу этого выражения. Для этого сначала узнаем форму неравенства Коши – Шварца :

${\ displaystyle \ | a ^ {\ mathrm {H}} b | ^ {2} \ leq (a ^ {\ mathrm {H}} a) (b ^ {\ mathrm {H}} b), \,}$

это означает, что квадрат внутреннего произведения двух векторов может быть только таким большим, как произведение отдельных внутренних произведений векторов. Эта концепция возвращается к интуиции, лежащей в основе согласованного фильтра: эта верхняя граница достигается, когда два вектора и параллельны. Мы возобновляем наш вывод, выражая верхнюю границу нашего в свете геометрического неравенства, приведенного выше: ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} \ leq {\ гидроразрыв {\ left [{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h) \ right] \ left [{(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s) \ right]} {{(R_ {v} ^ {1 / 2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}}.}.$

Наши отважные манипуляции с матрицей теперь окупились. Мы видим, что выражение для нашей верхней границы можно значительно упростить:

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} \ leq s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s.}$

Мы можем достичь этой верхней границы, если выберем

${\ displaystyle \ R_ {v} ^ {1/2} h = \ alpha R_ {v} ^ {- 1/2} s}$

где - произвольное действительное число. Чтобы проверить это, мы вставляем наше выражение для вывода : ${\ displaystyle \ alpha}$${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ mathrm {SNR} = {\ frac {| {(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s ) | ^ {2}} {{(R_ {v} ^ {1/2} h)} ^ {\ mathrm {H}} (R_ {v} ^ {1/2} h)}} = {\ frac {\ alpha ^ {2} | {(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s) | ^ {2 }} {\ alpha ^ {2} {(R_ {v} ^ {- 1/2} s)} ^ {\ mathrm {H}} (R_ {v} ^ {- 1/2} s)}} = {\ frac {| s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s | ^ {2}} {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s }} = s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s.}$

Таким образом, наш оптимальный согласованный фильтр

${\ displaystyle \ h = \ alpha R_ {v} ^ {- 1} s.}$

Мы часто предпочитаем нормализовать ожидаемое значение мощности выходного сигнала фильтра из-за шума до единицы. То есть мы сдерживаем

${\ Displaystyle \ E \ {| y_ {v} | ^ {2} \} = 1 \,}$

Это ограничение подразумевает значение , для которого мы можем решить: ${\ displaystyle \ alpha}$

${\ Displaystyle \ E \ {| y_ {v} | ^ {2} \} = \ alpha ^ {2} s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s = 1,}$

уступающий

${\ displaystyle \ \ alpha = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}},}$

давая нам нормализованный фильтр,

${\ displaystyle \ h = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}} R_ {v} ^ {- 1} s.}$

Если нам нужно записать импульсную характеристику фильтра для системы свертки, это будет просто комплексно-сопряженное обращение времени входа . ${\ displaystyle h}$${\ displaystyle s}$

Хотя мы получили согласованный фильтр в дискретном времени, мы можем расширить эту концепцию на системы с непрерывным временем, если мы заменим его автокорреляционной функцией непрерывного времени , предполагающей непрерывный сигнал , непрерывный шум и непрерывный фильтр . ${\ displaystyle R_ {v}}$${\ displaystyle s (t)}$${\ Displaystyle v (т)}$${\ Displaystyle ч (т)}$

Вывод через лагранжиан

В качестве альтернативы, мы можем решить для согласованного фильтра, решив нашу задачу максимизации с помощью лагранжиана. И снова согласованный фильтр стремится максимизировать отношение выходного сигнала к шуму ( ) отфильтрованного детерминированного сигнала в стохастическом аддитивном шуме. Наблюдаемая последовательность опять же ${\ displaystyle \ mathrm {SNR}}$

${\ Displaystyle \ х = s + v, \,}$

с ковариационной матрицей шума,

${\ Displaystyle \ R_ {v} = E \ {vv ^ {\ mathrm {H}} \}. \,}$

Отношение сигнал / шум равно

${\ displaystyle \ mathrm {SNR} = {\ frac {| y_ {s} | ^ {2}} {E \ {| y_ {v} | ^ {2} \}}},}$

где и . ${\ displaystyle y_ {s} = h ^ {\ mathrm {H}} s}$${\ displaystyle y_ {v} = h ^ {\ mathrm {H}} v}$

Оценивая выражение в числителе, имеем

${\ displaystyle \ | y_ {s} | ^ {2} = {y_ {s}} ^ {\ mathrm {H}} y_ {s} = h ^ {\ mathrm {H}} ss ^ {\ mathrm {H }} ч. \,}$

а в знаменателе

${\ Displaystyle \ E \ {| y_ {v} | ^ {2} \} = E \ {{y_ {v}} ^ {\ mathrm {H}} y_ {v} \} = E \ {h ^ { \ mathrm {H}} vv ^ {\ mathrm {H}} h \} = h ^ {\ mathrm {H}} R_ {v} h. \,}$

Отношение сигнал / шум становится

${\ displaystyle \ mathrm {SNR} = {\ frac {h ^ {\ mathrm {H}} ss ^ {\ mathrm {H}} h} {h ^ {\ mathrm {H}} R_ {v} h}} .}$

Если теперь ограничить знаменатель равным 1, проблема максимизации сведется к максимальному увеличению числителя. Затем мы можем сформулировать проблему, используя множитель Лагранжа : ${\ displaystyle \ mathrm {SNR}}$

${\ displaystyle \ h ^ {\ mathrm {H}} R_ {v} h = 1}$

${\ displaystyle \ {\ mathcal {L}} = h ^ {\ mathrm {H}} ss ^ {\ mathrm {H}} h + \ lambda (1-h ^ {\ mathrm {H}} R_ {v} h )}$

${\ displaystyle \ \ nabla _ {h ^ {*}} {\ mathcal {L}} = ss ^ {\ mathrm {H}} h- \ lambda R_ {v} h = 0}$

${\ displaystyle \ (ss ^ {\ mathrm {H}}) h = \ lambda R_ {v} h}$

которую мы распознаем как обобщенную проблему собственных значений

${\ displaystyle \ h ^ {\ mathrm {H}} (ss ^ {\ mathrm {H}}) h = \ lambda h ^ {\ mathrm {H}} R_ {v} h.}$

Поскольку он имеет единичный ранг, он имеет только одно ненулевое собственное значение. Можно показать, что это собственное значение равно ${\ displaystyle ss ^ {\ mathrm {H}}}$

${\ displaystyle \ \ lambda _ {\ max} = s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s,}$

давая следующий оптимальный согласованный фильтр

${\ displaystyle \ h = {\ frac {1} {\ sqrt {s ^ {\ mathrm {H}} R_ {v} ^ {- 1} s}}} R_ {v} ^ {- 1} s.}$

Это тот же результат, что и в предыдущем подразделе.

Интерпретация как оценка методом наименьших квадратов

Вывод

Согласованная фильтрация также может интерпретироваться как оценка методом наименьших квадратов для оптимального расположения и масштабирования данной модели или шаблона. Еще раз, пусть наблюдаемая последовательность определяется как

${\ displaystyle \ x_ {k} = s_ {k} + v_ {k}, \,}$

где - некоррелированный шум с нулевым средним. Предполагается, что сигнал является масштабированной и сдвинутой версией известной модельной последовательности : ${\ displaystyle v_ {k}}$${\ displaystyle s_ {k}}$${\ displaystyle f_ {k}}$

${\ displaystyle \ s_ {k} = \ mu _ {0} \ cdot f_ {k-j_ {0}}}$

Мы хотим найти оптимальные оценки и для неизвестного сдвига и масштабирования , минимизируя остаток методом наименьших квадратов между наблюдаемой последовательностью и «проверочной последовательностью» : ${\ displaystyle j ^ {*}}$${\ Displaystyle \ mu ^ {*}}$${\ displaystyle j_ {0}}$${\ displaystyle \ mu _ {0}}$${\ displaystyle x_ {k}}$${\ displaystyle h_ {jk}}$

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ min _ {j, \ mu} \ sum _ {k} \ left (x_ {k} - \ mu \ cdot h_ {jk} \ right) ^ {2}}$

Соответствующий фильтр позже окажется согласованным фильтром, но он еще не определен. Расширение и квадрат внутри суммы дают ${\ displaystyle h_ {jk}}$${\ displaystyle x_ {k}}$

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ min _ {j, \ mu} \ left [\ sum _ {k} (s_ {k} + v_ {k}) ^ { 2} + \ mu ^ {2} \ sum _ {k} h_ {jk} ^ {2} -2 \ mu \ sum _ {k} s_ {k} h_ {jk} -2 \ mu \ sum _ {k } v_ {k} h_ {jk} \ right]}$ .

Первый член в скобках является константой (поскольку дается наблюдаемый сигнал) и не влияет на оптимальное решение. Последний член имеет постоянное ожидаемое значение, потому что шум некоррелирован и имеет нулевое среднее значение. Таким образом, мы можем исключить оба термина из оптимизации. Поменяв знак на противоположный, получим эквивалентную задачу оптимизации

${\ displaystyle \ j ^ {*}, \ mu ^ {*} = \ arg \ max _ {j, \ mu} \ left [2 \ mu \ sum _ {k} s_ {k} h_ {jk} - \ mu ^ {2} \ sum _ {k} h_ {jk} ^ {2} \ right]}$ .

Установка производной по отношению к нулю дает аналитическое решение для : ${\ displaystyle \ mu}$${\ Displaystyle \ mu ^ {*}}$

${\ displaystyle \ \ mu ^ {*} = {\ frac {\ sum _ {k} s_ {k} h_ {jk}} {\ sum _ {k} h_ {jk} ^ {2}}}}$ .

Вставка этого в нашу целевую функцию дает сокращенную задачу максимизации всего за : ${\ displaystyle j ^ {*}}$

${\ displaystyle \ j ^ {*} = \ arg \ max _ {j} {\ frac {\ left (\ sum _ {k} s_ {k} h_ {jk} \ right) ^ {2}} {\ sum _ {k} h_ {jk} ^ {2}}}}$ .

Числитель можно ограничить сверху с помощью неравенства Коши – Шварца :

${\ displaystyle \ {\ frac {\ left (\ sum _ {k} s_ {k} h_ {jk} \ right) ^ {2}} {\ sum _ {k} h_ {jk} ^ {2}}} \ leq {\ frac {\ sum _ {k} s_ {k} ^ {2} \ cdot \ sum _ {k} h_ {jk} ^ {2}} {\ sum _ {k} h_ {jk} ^ { 2}}} = \ сумма _ {k} s_ {k} ^ {2} = \ mathrm {const}}$ .

Задача оптимизации принимает максимум, когда в этом выражении выполняется равенство. Согласно свойствам неравенства Коши – Шварца это возможно только при

${\ displaystyle \ h_ {jk} = \ nu \ cdot s_ {k} = \ kappa \ cdot f_ {k-j_ {0}}}$ .

для произвольных ненулевых констант или , и оптимальное решение получается при желаемом. Таким образом, наша «последовательность зондирования» должна быть пропорциональна модели сигнала , и удобный выбор дает согласованный фильтр. ${\ displaystyle \ nu}$${\ displaystyle \ kappa}$${\ displaystyle j ^ {*} = j_ {0}}$${\ displaystyle h_ {jk}}$${\ displaystyle f_ {k-j_ {0}}}$${\ displaystyle \ kappa = 1}$

${\ displaystyle \ h_ {k} = f _ {- k}}$ .

Обратите внимание, что фильтр является зеркальной моделью сигнала. Это гарантирует, что операция, применяемая для поиска оптимума, действительно является сверткой между наблюдаемой последовательностью и согласованным фильтром . Отфильтрованная последовательность предполагает максимум в том месте, где наблюдаемая последовательность наилучшим образом соответствует (в смысле наименьших квадратов) модели сигнала . ${\ displaystyle \ sum _ {k} x_ {k} h_ {jk}}$${\ displaystyle x_ {k}}$${\ displaystyle h_ {k}}$${\ displaystyle x_ {k}}$${\ displaystyle f_ {k}}$

Подразумеваемое

Согласованный фильтр может быть получен множеством способов, но как частный случай процедуры наименьших квадратов его также можно интерпретировать как метод максимального правдоподобия в контексте модели (цветного) гауссовского шума и связанной с ним вероятности Уиттла . Если передаваемый сигнал не имеет неизвестных параметров (таких как время прихода, амплитуда и т. Д.), То согласованный фильтр, согласно лемме Неймана – Пирсона , минимизирует вероятность ошибки. Однако, поскольку точный сигнал обычно определяется неизвестными параметрами, которые эффективно оцениваются (или подгоняются ) в процессе фильтрации, согласованный фильтр представляет собой обобщенную статистику максимального правдоподобия (тестовую). Отфильтрованные временные ряды затем можно интерпретировать как (пропорционально) вероятности профиля , максимальной условной вероятности как функции параметра времени. Это, в частности, означает, что вероятность ошибки (в смысле Неймана и Пирсона, т. Е. Относительно максимизации вероятности обнаружения для данной вероятности ложной тревоги) не обязательно оптимальна. То, что обычно называют отношением сигнал / шум (SNR) , которое должно быть максимизировано согласованным фильтром, в этом контексте соответствует , где - (условно) максимальное отношение правдоподобия. ${\ displaystyle {\ sqrt {2 \ log ({\ mathcal {L}})}}}$${\ Displaystyle {\ mathcal {L}}}$

Конструкция согласованного фильтра основана на известном спектре шума . В действительности, однако, спектр шума обычно оценивается по данным и, следовательно, известен только с ограниченной точностью. Для случая неопределенного спектра согласованный фильтр может быть обобщен до более надежной итерационной процедуры с благоприятными свойствами также в негауссовском шуме.

Интерпретация в частотной области

При рассмотрении в частотной области очевидно, что согласованный фильтр применяет наибольшее взвешивание к спектральным компонентам, демонстрирующим наибольшее отношение сигнал / шум (т. Е. Большой вес при относительно низком уровне шума, и наоборот). Как правило, для этого требуется непрямая частотная характеристика, но связанное с этим "искажение" не является поводом для беспокойства в таких ситуациях, как радар и цифровая связь , где исходная форма волны известна, а целью является обнаружение этого сигнала на фоне фонового шума. . С технической стороны согласованный фильтр представляет собой взвешенный метод наименьших квадратов, основанный на ( гетероскедастических ) данных частотной области (где «веса» определяются через спектр шума, см. Также предыдущий раздел) или, что то же самое, наименьшее - к отбеленным данным применен метод квадратов .

Примеры

Согласованный фильтр в радаре и гидролокаторе

Согласованные фильтры часто используются при обнаружении сигналов . В качестве примера предположим, что мы хотим судить о расстоянии до объекта, отражая от него сигнал. Мы можем выбрать передачу синусоиды чистого тона с частотой 1 Гц. Мы предполагаем, что наш принятый сигнал представляет собой ослабленную и сдвинутую по фазе форму переданного сигнала с добавленным шумом.

Чтобы судить о расстоянии до объекта, мы коррелируем полученный сигнал с согласованным фильтром, который в случае белого (некоррелированного) шума является еще одной синусоидой 1 Гц с чистым тоном. Когда выходной сигнал согласованной системы фильтров превышает определенный порог, мы с высокой вероятностью заключаем, что принятый сигнал отражен от объекта. Используя скорость распространения и время, в которое мы впервые наблюдаем отраженный сигнал, мы можем оценить расстояние до объекта. Если мы изменим форму импульса специально разработанным способом, отношение сигнал / шум и разрешение по расстоянию можно будет даже улучшить после согласованной фильтрации: это метод, известный как сжатие импульсов .

Кроме того, согласованные фильтры могут использоваться в задачах оценки параметров (см. Теорию оценивания ). Чтобы вернуться к нашему предыдущему примеру, мы можем захотеть оценить скорость объекта в дополнение к его положению. Чтобы использовать эффект Доплера , мы хотели бы оценить частоту принимаемого сигнала. Для этого мы можем коррелировать принятый сигнал с несколькими согласованными фильтрами синусоид на различных частотах. Согласованный фильтр с максимальной выходной мощностью с большой вероятностью обнаружит частоту отраженного сигнала и поможет нам определить скорость объекта. Фактически, этот метод является простой версией дискретного преобразования Фурье (ДПФ) . ДПФ принимает комплексный вход с двумя значениями и коррелирует его с согласованными фильтрами, соответствующими комплексным экспонентам на разных частотах, чтобы получить комплексные числа, соответствующие относительным амплитудам и фазам синусоидальных компонентов (см. Индикация движущейся цели ). ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle N}$

Согласованный фильтр в цифровой связи

Согласованный фильтр также используется в коммуникациях. В контексте системы связи, которая отправляет двоичные сообщения от передатчика к приемнику по зашумленному каналу, согласованный фильтр может использоваться для обнаружения переданных импульсов в зашумленном принятом сигнале.

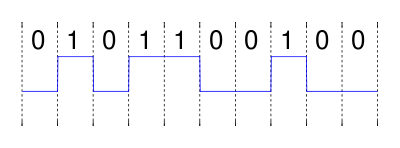
Представьте, что мы хотим отправить последовательность «0101100100», закодированную в неполярном без возврата к нулю (NRZ), через определенный канал.

Математически последовательность в коде NRZ может быть описана как последовательность единичных импульсов или сдвинутых прямоугольных функций , при этом каждый импульс взвешивается на +1, если бит равен «1», и на -1, если бит равен «0». Формально коэффициент масштабирования для долота равен, ${\ Displaystyle к ^ {\ mathrm {th}}}$

${\ displaystyle \ a_ {k} = {\ begin {case} +1, & {\ mbox {if bit}} k {\ mbox {is 1}}, \\ - 1, & {\ mbox {if bit} } k {\ mbox {0}}. \ end {case}}}$

Мы можем представить наше сообщение как сумму сдвинутых единичных импульсов: ${\ Displaystyle M (т)}$

${\ Displaystyle \ M (T) = \ сумма _ {к = - \ infty} ^ {\ infty} a_ {k} \ times \ Pi \ left ({\ frac {t-kT} {T}} \ right) .}$

где - длина одного бита. ${\ displaystyle T}$

Таким образом, сигнал, который должен послать передатчик,

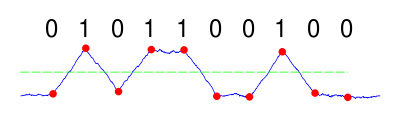
Если мы моделируем наш зашумленный канал как канал AWGN , к сигналу добавляется белый гауссовский шум. На стороне приемника для отношения сигнал / шум 3 дБ это может выглядеть так:

Первый взгляд не покажет исходную переданную последовательность. Уровень шума выше мощности полезного сигнала (т. Е. Отношение сигнал / шум низкое ). Если бы приемник отбирал этот сигнал в правильные моменты, результирующее двоичное сообщение могло бы противоречить исходному переданному.

Чтобы увеличить отношение сигнал / шум, мы пропускаем полученный сигнал через согласованный фильтр. В этом случае фильтр должен быть согласован с импульсом NRZ (эквивалентным «1», закодированной в коде NRZ). Точнее говоря, импульсная характеристика идеального согласованного фильтра, предполагающая белый (некоррелированный) шум, должна быть масштабированной комплексно-сопряженной версией сигнала, который мы ищем, с обращенной во времени. Мы выбрали

${\ displaystyle \ h (t) = \ Pi \ left ({\ frac {t} {T}} \ right).}$

В этом случае из-за симметрии обращенное во времени комплексное сопряжение равно фактически , что позволяет нам вызывать импульсную характеристику нашей системы свертки согласованного фильтра. ${\ Displaystyle ч (т)}$${\ Displaystyle ч (т)}$${\ Displaystyle ч (т)}$

После свертки с правильным согласованным фильтром результирующий сигнал будет ${\ Displaystyle М _ {\ mathrm {отфильтрованный}} (т)}$

${\ Displaystyle \ M _ {\ mathrm {отфильтрованный}} (т) = М (т) * ч (т)}$

где обозначает свертку. ${\ displaystyle *}$

Который теперь может быть безопасно выбран приемником в правильные моменты выборки и сравнен с соответствующим порогом, что приводит к правильной интерпретации двоичного сообщения.

Согласованный фильтр в гравитационно-волновой астрономии

Согласованные фильтры играют центральную роль в гравитационно-волновой астрономии . Первое наблюдение гравитационных волн было основано на крупномасштабной фильтрации выхода каждого детектора для сигналов , напоминающих ожидаемой форму, а затем последующим скринингом на совпадающие и согласованные триггера между обеими инструментами. Частота ложных тревог и, соответственно, статистическая значимость обнаружения были затем оценены с использованием методов повторной выборки . Вывод о параметрах астрофизических источников был завершен с использованием байесовских методов, основанных на параметризованных теоретических моделях для формы сигнала и (опять же) на вероятности Уиттла .

Смотрите также

• Периодограмма
• Отфильтрованная обратная проекция (преобразование Радона)
• Цифровой фильтр
• Статистическая обработка сигналов
• Малая вероятность
• Вероятность профиля
• Теория обнаружения
• Проблема множественных сравнений
• Емкость канала
• Теорема кодирования с шумом
• Оценка спектральной плотности
• Фильтр наименьших средних квадратов (LMS)
• Фильтр Винера
• MUltiple SIgnal Classification (MUSIC), популярный параметрический метод сверхразрешения
• САМВ

Заметки

Рекомендации

дальнейшее чтение

• Турин, ГЛ (1960). «Введение в согласованные фильтры» . Сделки IRE по теории информации . 6 (3): 311–329. DOI : 10.1109 / TIT.1960.1057571 .
• Вайнштейн, штат Луизиана; Зубаков, В.Д. (1962). Выделение сигналов из шума . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл .
• Мелвин, WL (2004). «Обзор STAP». Журнал IEEE Aerospace and Electronic Systems Magazine . 19 (1): 19–35. DOI : 10,1109 / MAES.2004.1263229 .
• Рёвер, К. (2011). «Фильтр Стьюдента для надежного обнаружения сигнала». Physical Review D . 84 (12): 122004. arXiv : 1109.0442 . Bibcode : 2011PhRvD..84l2004R . DOI : 10.1103 / PhysRevD.84.122004 .
• Fish, A .; Гуревич, С .; Hadani, R .; Sayeed, A .; Шварц, О. (декабрь 2011 г.). «Вычисление согласованного фильтра за линейное время». arXiv : 1112.4883 [ cs.IT ].