Теорема о пицце - Pizza theorem

Пример применения теоремы с восемью секторами: разрезая пиццу вдоль синих линий и, поочередно беря по кусочку каждый, действуя по или против часовой стрелки, двое посетителей съедают одинаковое количество (измеренное по площади) пиццы.
Доказательство без слов для 8 секторов Картера и Вагона (1994a) .

В элементарной геометрии теорема о пицце утверждает равенство двух областей, которые возникают, когда диск разбивается определенным образом.

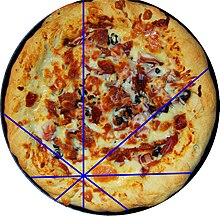
Пусть p - внутренняя точка диска, и пусть n кратно 4 и больше или равно 8. Сформируйте n секторов диска с равными углами, выбрав произвольную прямую через p , вращая линию п/2 - 1 раз под углом2 π/п радиан и разрезая диск на каждый из полученныхп/2линий. Пронумеруйте сектора последовательно по или против часовой стрелки. Тогда теорема о пицце утверждает, что:

Сумма площадей секторов с нечетными номерами равна сумме площадей секторов с четными номерами ( Аптон, 1968 ).

Теорема о пицце называется так потому, что имитирует традиционную технику нарезки пиццы . Это показывает, что если два человека делят пиццу, нарезанную таким образом, чередуя кусочки, то каждый из них получает одинаковое количество пиццы.

История

Теорема о пицце была первоначально предложена Аптоном (1967) как проблема . Опубликованное решение этой проблемы Майклом Голдбергом включало прямую манипуляцию алгебраическими выражениями для площадей секторов. Картер и Вагон (1994a) предлагают альтернативное доказательство путем вскрытия . Они показывают, как разделить секторы на более мелкие части, чтобы каждая часть в секторе с нечетным номером имела конгруэнтную часть в секторе с четным номером, и наоборот. Фредериксон (2012) дал семейство доказательств вскрытия для всех случаев (в которых количество секторов составляет 8, 12, 16, ... ).

Обобщения

12 секторов: зеленая зона = оранжевая зона

Требование, чтобы количество секторов было кратным четырем, необходимо: как показал Дон Копперсмит , разделение диска на четыре сектора или количество секторов, которое не делится на четыре, в целом не дает равных площадей. Mabry & Deiermann (2009) ответили на проблему Carter & Wagon (1994b) , предоставив более точную версию теоремы, которая определяет, какой из двух наборов секторов имеет большую площадь в случаях, когда площади неравны. В частности, если количество секторов равно 2 (mod 8) и ни один срез не проходит через центр диска, то подмножество срезов, содержащее центр, имеет меньшую площадь, чем другое подмножество, в то время как если количество секторов равно 6 (mod 8) и ни один срез не проходит через центр, тогда подмножество срезов, содержащее центр, имеет большую площадь. Нечетное количество секторов невозможно при прямолинейных разрезах, а разрез через центр приводит к тому, что два подмножества становятся равными независимо от количества секторов.

Mabry & Deiermann (2009) также отмечают, что, когда пицца делится равномерно, то же самое происходит и с ее коркой (корку можно интерпретировать либо как периметр диска, либо как область между границей диска и меньшим кругом, имеющим обозначение один и тот же центр, с точкой разреза, лежащей внутри последнего), и поскольку диски, ограниченные обеими окружностями, разделены равномерно, такова и их разница. Однако, когда пицца делится неравномерно, тот, кто получает больше всего пиццы, на самом деле получает меньше всего корочки.

Как Hirschhorn et al. (1999) отмечают, что равное разделение пиццы также приводит к равному разделению ее начинки, если каждая начинка распределена на диске (не обязательно концентрично со всей пиццей), который содержит центральную точку p разделения на секторов.

Связанные результаты

Hirschhorn et al. (1999) показывают, что пицца, нарезанная так же, как в теореме о пицце, на количество n секторов с равными углами, где n делится на четыре, также может быть разделена поровну между n / 4 людьми. Например, пицца, разделенная на 12 секторов, может быть разделена поровну как тремя людьми, так и двумя; однако, чтобы вместить все пять Хиршхорнов, пиццу необходимо разделить на 20 секторов.

Cibulka et al. (2010) и Knauer, Micek & Ueckerdt (2011) изучают теорию игр о выборе бесплатных кусочков пиццы, чтобы гарантировать большую долю, - проблема, поставленная Дэном Брауном и Питером Винклером . В изучаемой ими версии задачи пицца нарезается радиально (без гарантии наличия секторов с равными углами), и двое посетителей поочередно выбирают кусочки пиццы, прилегающие к уже съеденному участку. Если двое посетителей пытаются увеличить количество пиццы, которое они съедают, посетитель, который берет первый кусок, может гарантировать 4/9 доли от общего количества пиццы, и существует такой кусок пиццы, что он не может взять больше. В задаче справедливого деления или разрезания торта рассматриваются похожие игры, в которых разные игроки имеют разные критерии измерения размера своей доли; например, один посетитель может предпочесть съесть больше пепперони, а другой - больше сыра.

Смотрите также

Другие математические результаты, связанные с нарезкой пиццы, включают последовательность ленивого поставщика еды , последовательность целых чисел, которая подсчитывает максимальное количество кусочков пиццы, которое можно получить заданным количеством прямых ломтиков, и теорему о сэндвиче с ветчиной , результат о нарезке трех -мерные объекты, двумерная версия которых подразумевает, что любая пицца, независимо от ее деформации, может иметь свою площадь и длину корки одновременно, разделенные пополам одним тщательно выбранным прямолинейным разрезом, и чья трехмерная версия подразумевает, что существует плоский разрез который в равной степени разделяет базу, помидоры и сыр.

использованная литература

  • Картер, Ларри; Вагон, Стэн (1994a), "Доказательство без слов: справедливое распределение пиццы", Математика Magazine , 67 (4): 267, DOI : 10,1080 / 0025570X.1994.11996228 , JSTOR  2690845.
  • Картер, Ларри; Вагон, Стэн (1994b), «Задача 1457», Mathematics Magazine , 67 (4): 303–310, JSTOR  2690855.
  • Цибулка, Йозеф; Кинчл, Ян; Месарош, Альт; Столарж, Рудольф; Валтр, Павел (2010), «Решение проблемы Питера Винклера о пицце», Фет комбинаторики и информатики , Математические исследования Общества Бойяи, 20 , Математическое общество Яноша Бойяи и Springer-Verlag, стр. 63–93, arXiv : 0812.4322 , doi : 10.1007 / 978-3-642-13580-4_4 , ISBN 978-3-642-13579-8, S2CID  18272355.
  • Hirschhorn, J .; Хиршхорн, доктор медицины; Hirschhorn, JK; Hirschhorn, AD; Хиршхорн, П.М. Хиршхорн (1999), "Теорема о пицце" (PDF) , Austral. Математика. Soc. Газ. , 26 : 120–121.
  • Фредериксон, Грег (2012), «Доказательство в пицце», Mathematics Magazine , 85 (1): 26–33, doi : 10.4169 / math.mag.85.1.26 , JSTOR  10.4169 / math.mag.85.1.26 , S2CID  116636161.
  • Кнауэр, Коля; Мичек, Петр; Ueckerdt, Torsten (2011), «Как съесть 4/9 пиццы», Дискретная математика , 311 (16): 1635–1645, arXiv : 0812.2870 , doi : 10.1016 / j.disc.2011.03.015 , S2CID  15566728.
  • Мабри, Рик; Deiermann, Павел (2009), "Из сыра и Корка: Доказательство Pizza гипотезы и других вкусных результатов", American Mathematical Monthly , 116 (5): 423-438, DOI : 10,4169 / 193009709x470317 , JSTOR  40391118.
  • Орнес, Стивен (11 декабря 2009 г.), «Идеальный способ нарезать пиццу» , New Scientist.
  • Аптон, LJ (1967), «Проблема 660», Mathematics Magazine , 40 (3): 163, JSTOR  2688484 . Постановка задачиCS1 maint: postscript ( ссылка ).
  • Аптон, LJ (1968), «Проблема 660», Mathematics Magazine , 41 (1): 42, JSTOR  2687962 . Решение Майкла ГолдбергаCS1 maint: postscript ( ссылка ).
  • Бержени, Джордж (1994), "Теорема о пицце - Часть I" (PDF) , Quantum Magazine : 29
  • Бержени, Джордж (1994), "Теорема о пицце - Часть II" (PDF) , Quantum Magazine : 29

внешние ссылки