Задача кратчайшего пути - Shortest path problem

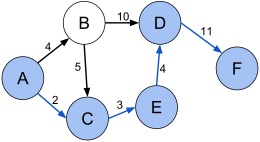
Кратчайший путь (A, C, E, D, F) между вершинами A и F взвешенного ориентированного графа

В теории графов , то задача о кратчайшем пути является проблема нахождения пути между двумя вершинами (или узлами) в графе таким образом, что сумма весов входящих в него ребер сведено к минимуму.

Задача поиска кратчайшего пути между двумя перекрестками на дорожной карте может быть смоделирована как частный случай задачи кратчайшего пути в графах, где вершины соответствуют перекресткам, а края соответствуют сегментам дороги, каждый из которых взвешен по длине проезжей части. сегмент.

Определение

Задача о кратчайшем пути может быть определена для графов ли неориентированный , направленных , или смешанные . Здесь он определен для неориентированных графов; для ориентированных графов определение пути требует, чтобы последовательные вершины были соединены соответствующим ориентированным ребром.

Две вершины смежны, если обе инцидентны общему ребру. Путь в неориентированном графе является последовательностью вершин таким образом, что примыкает к для . Такой путь называется путем длиной от до . (Это переменные; их нумерация здесь связана с их положением в последовательности и не обязательно должна иметь отношение к какой-либо канонической маркировке вершин.) ${\ displaystyle P = (v_ {1}, v_ {2}, \ ldots, v_ {n}) \ in V \ times V \ times \ cdots \ times V}$ ${\ displaystyle v_ {i}}$ ${\ displaystyle v_ {я + 1}}$ ${\ Displaystyle 1 \ Leq я <п}$ ${\ displaystyle P}$ ${\ displaystyle n-1}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {n}}$ ${\ displaystyle v_ {i}}$

Позвольте быть ребром, инцидентным обоим и . Учитывая действительную весовую функцию и неориентированный (простой) граф , кратчайший путь от до - это путь (где и ), который по всем возможным минимизирует сумму.Когда каждое ребро в графе имеет единичный вес или , это эквивалентно поиск пути с наименьшим количеством краев. ${\ displaystyle e_ {i, j}}$ ${\ displaystyle v_ {i}}$ ${\ displaystyle v_ {j}}$ ${\ displaystyle f: E \ rightarrow \ mathbb {R}}$ ${\ displaystyle G}$ ${\ displaystyle v}$ ${\ displaystyle v '}$ ${\ Displaystyle P = (v_ {1}, v_ {2}, \ ldots, v_ {n})}$ ${\ displaystyle v_ {1} = v}$ ${\ displaystyle v_ {n} = v '}$ ${\ displaystyle n}$ ${\ displaystyle \ sum _ {i = 1} ^ {n-1} f (e_ {i, i + 1}).}$ ${\ displaystyle f: E \ rightarrow \ {1 \}}$

Эту проблему также иногда называют проблемой кратчайшего пути для одной пары , чтобы отличить ее от следующих вариантов:

Одним источником проблем короткий путь , в котором мы должны найти кратчайшие пути из исходной вершины V для всех остальных вершин в графе.
Задача кратчайшего пути с одним адресатом , в которой мы должны найти кратчайшие пути от всех вершин ориентированного графа к одной конечной вершине v . Это можно свести к задаче поиска кратчайшего пути с одним источником путем обращения дуг в ориентированном графе.
Задача поиска кратчайшего пути для всех пар , в которой мы должны найти кратчайший путь между каждой парой вершин v , v ' в графе.

Эти обобщения имеют значительно более эффективные алгоритмы, чем упрощенный подход к запуску алгоритма кратчайшего пути для одной пары на всех соответствующих парах вершин.

Алгоритмы

Наиболее важные алгоритмы решения этой проблемы:

Алгоритм Дейкстры решает проблему кратчайшего пути с одним источником с неотрицательным весом ребра.
Алгоритм Беллмана – Форда решает проблему единственного источника, если веса ребер могут быть отрицательными.
Алгоритм поиска * решает кратчайший путь из одной пары с помощью эвристики, чтобы попытаться ускорить поиск.
Алгоритм Флойда – Уоршалла решает все пары кратчайших путей.
Алгоритм Джонсона решает все пары кратчайших путей и может быть быстрее, чем алгоритм Флойда – Уоршалла на разреженных графах .
Алгоритм Витерби решает задачу о кратчайшем стохастическом пути с дополнительным вероятностным весом на каждом узле.

Дополнительные алгоритмы и связанные с ними оценки можно найти в Cherkassky, Goldberg & Radzik (1996) .

Кратчайшие пути из одного источника

Ненаправленные графы

Вес	Сложность времени	Автор
ℝ ₊	O ( V ² )	Дейкстра 1959
ℝ ₊	O (( E + V ) журнал V )	Джонсон 1977 ( двоичная куча )
ℝ ₊	O ( E + V журнал V )	Фредман и Тарьян 1984 ( куча Фибоначчи )
ℕ	O ( E )	Thorup 1999 (требуется постоянное умножение)

Невзвешенные графики

Алгоритм	Сложность времени	Автор
Поиск в ширину	O ( E + V )

Направленные ациклические графы (DAG)

Алгоритм, использующий топологическую сортировку, может решить проблему кратчайшего пути с одним источником за время $Θ (E + V)$ в произвольно взвешенных группах DAG.

Направленные графы с неотрицательными весами

Следующая таблица взята из Schrijver (2004) с некоторыми исправлениями и дополнениями. Зеленый фон указывает на асимптотически наилучшую границу в таблице; L - максимальная длина (или вес) среди всех ребер с учетом целочисленных весов ребер.

Вес	Алгоритм	Сложность времени	Автор
ℝ		O ( V ²EL )	Ford 1956 года
ℝ	Алгоритм Беллмана – Форда	O ( VE )	Шимбел 1955 , Беллман 1958 , Мур 1959
ℝ		O ( V ² log V )	Данциг 1960
ℝ	Алгоритм Дейкстры со списком	O ( V ² )	Leyzorek et al. 1957 , Dijkstra 1959 , Minty (см. Pollack & Wiebenson 1960 ), Whiting & Hillier 1960
ℝ	Алгоритм Дейкстры с двоичной кучей	O (( E + V ) журнал V )	Джонсон 1977
ℝ	Алгоритм Дейкстры с кучей Фибоначчи	O ( E + V журнал V )	Фредман и Тарьян 1984 , Фредман и Тарьян 1987
ℕ	Алгоритм Dial (алгоритм Дейкстры с использованием очереди ведра с L корзинами)	O ( E + LV )	Набери 1969
		O ( E log log L )	Джонсон 1981 , Карлссон и Поблете 1983
	Алгоритм Габоу	O ( E log _{E / V} L )	Габоу 1983 , Габоу 1985
		O ( E + V √ журнал L )	Ахуджа и др. 1990 г.
	Thorup	O ( E + V журнал журнал V )	Thorup 2004

Направленные графы с произвольными весами без отрицательных циклов

Вес	Алгоритм	Сложность времени	Автор
ℝ		O ( V ²EL )	Ford 1956 года
ℝ	Алгоритм Беллмана – Форда	O ( VE )	Шимбел 1955 , Беллман 1958 , Мур 1959
ℝ	Джонсон-Дейкстра с двоичной кучей	O ( V ( E + журнал V ))	Джонсон 1977
ℝ	Джонсон-Дейкстра с кучей Фибоначчи	O ( V ( E + журнал V ))	Фредман и Тарджан 1984 , Фредман и Тарджан 1987 , адаптировано по Джонсону 1977 года.
ℕ	Техника Джонсона, примененная к алгоритму Диала	O ( V ( E + L ))	Наберите 1969 г. , адаптированный после Джонсона 1977 г.

Плоские ориентированные графы с произвольными весами

Кратчайшие пути для всех пар

Задача поиска кратчайшего пути для всех пар находит кратчайшие пути между каждой парой вершин $v$ , $v '$ в графе. Задача поиска кратчайших путей для всех пар для невзвешенных ориентированных графов была введена Шимбелем (1953) , который заметил, что ее можно решить с помощью линейного числа умножений матриц, что в целом занимает $O (V 4)$ .

Ненаправленный граф

Вес	Сложность времени	Алгоритм
ℝ ₊	$O (V 3)$	Алгоритм Флойда-Уоршолла
${\ displaystyle \ {1, \ infty \}}$	${\ Displaystyle O (V ^ {\ omega} \ log V)}$	Алгоритм Зейделя (ожидаемое время работы)
ℕ	${\ Displaystyle О (V ^ {3} / 2 ^ {\ Omega (\ log n) ^ {1/2}})}$	Уильямс 2014
ℝ ₊	$O (EV журнал α (E, V))$	Петти и Рамачандран 2002
ℕ	$O (EV)$	Thorup 1999 применяется к каждой вершине (требуется постоянное умножение).

Направленный граф

Вес	Сложность времени	Алгоритм
ℝ (без отрицательных циклов)	$O (V 3)$	Алгоритм Флойда-Уоршолла
ℕ	${\ Displaystyle О (V ^ {3} / 2 ^ {\ Omega (\ log n) ^ {1/2}})}$	Уильямс 2014
ℝ (без отрицательных циклов)	$O (EV + V 2 log V)$	Джонсон-Дейкстра
ℝ (без отрицательных циклов)	$O (EV + V 2 log log V)$	Петти 2004
ℕ	$O (EV + V 2 log log V)$	Hagerup 2000

Приложения

Алгоритмы кратчайшего пути применяются для автоматического поиска направлений между физическими точками, например маршрутов проезда на веб-картографических веб-сайтах, таких как MapQuest или Google Maps . Для этого приложения доступны быстрые специализированные алгоритмы.

Если представить недетерминированную абстрактную машину в виде графа, в котором вершины описывают состояния, а ребра описывают возможные переходы, можно использовать алгоритмы кратчайшего пути, чтобы найти оптимальную последовательность вариантов для достижения определенного состояния цели или установить нижние границы времени, необходимого для достичь заданного состояния. Например, если вершины представляют состояния головоломки, такой как кубик Рубика, и каждое направленное ребро соответствует одному движению или повороту, можно использовать алгоритмы кратчайшего пути, чтобы найти решение, которое использует минимально возможное количество ходов.

В сетевом или телекоммуникационном мышлении эту проблему кратчайшего пути иногда называют проблемой минимальной задержки и обычно связывают с проблемой самого широкого пути . Например, алгоритм может искать самый короткий (минимальная задержка) самый широкий путь или самый широкий самый короткий путь (минимальная задержка).

Более легкое применение - игры « шести степеней разделения », которые пытаются найти кратчайший путь на графиках, как кинозвезды, появляющиеся в одном фильме.

Другие приложения, которые часто изучаются при исследовании операций , включают компоновку завода и объекта, робототехнику , транспорт и проектирование СБИС .

Дорожные сети

Дорожную сеть можно рассматривать как граф с положительными весами. Узлы представляют собой дорожные развязки, и каждое ребро графа связано с участком дороги между двумя перекрестками. Вес края может соответствовать длине соответствующего сегмента дороги, времени, необходимому для прохождения сегмента, или стоимости пересечения сегмента. Используя направленные кромки, также можно моделировать улицы с односторонним движением. Такие графы являются особенными в том смысле, что некоторые ребра важнее других для дальних путешествий (например, автомагистралей). Это свойство было формализовано с использованием понятия размерности автомагистрали. Существует множество алгоритмов, которые используют это свойство и поэтому могут вычислять кратчайший путь намного быстрее, чем это было бы возможно на общих графах.

Все эти алгоритмы работают в два этапа. На первом этапе граф предварительно обрабатывается без знания исходного или целевого узла. Второй этап - это этап запроса. На этом этапе известны исходный и целевой узел. Идея состоит в том, что дорожная сеть является статической, поэтому этап предварительной обработки можно выполнить один раз и использовать для большого количества запросов в одной и той же дорожной сети.

Алгоритм с самым быстрым известным временем запроса называется разметкой концентраторов и может вычислять кратчайший путь в дорожных сетях Европы или США за доли микросекунды. Другие использованные методы:

ALT ( поиск A * , ориентиры и неравенство треугольника )
Флаги дуги
Иерархии сжатия
Маршрутизация транзитного узла
Обрезка по досягаемости
Маркировка
Ярлыки концентраторов

Связанные проблемы

Для получения информации о задачах кратчайшего пути в вычислительной геометрии см. Евклидов кратчайший путь .

Задача коммивояжера - это задача найти кратчайший путь, который проходит через каждую вершину ровно один раз и возвращается в начало. В отличие от задачи о кратчайшем пути, которая может быть решена за полиномиальное время в графах без отрицательных циклов, задача коммивояжера является NP-полной и, как таковая, считается неэффективно решаемой для больших наборов данных (см. P = NP проблема ). Задача поиска самого длинного пути в графе также является NP-полной.

Проблема канадского путешественника и проблема стохастического кратчайшего пути - это обобщения, в которых либо граф не полностью известен движущемуся, изменяется со временем, либо действия (обходы) являются вероятностными.

Кратчайший путь с несколькими отключениями - это представление сети примитивных путей в рамках теории Рептаций .

Задача самого широкого пути ищет такой путь, чтобы минимальная метка любого ребра была как можно больше.

Стратегические кратчайшие пути

Иногда у ребер графа есть индивидуальности: каждое ребро имеет свой эгоистичный интерес. Примером может служить сеть связи, в которой каждое ребро представляет собой компьютер, который, возможно, принадлежит другому человеку. Разные компьютеры имеют разную скорость передачи, поэтому каждое ребро в сети имеет числовой вес, равный количеству миллисекунд, необходимых для передачи сообщения. Наша цель - отправить сообщение между двумя точками сети в кратчайшие сроки. Если мы знаем время передачи каждого компьютера (вес каждого ребра), то мы можем использовать стандартный алгоритм поиска кратчайших путей. Если мы не знаем время передачи, мы должны попросить каждый компьютер сообщить нам свое время передачи. Но компьютеры могут быть эгоистичными: компьютер может сказать нам, что время его передачи очень велико, так что мы не будем беспокоить его своими сообщениями. Возможное решение этой проблемы - использовать вариант механизма VCG , который дает компьютерам стимул раскрывать свой истинный вес.

Формулировка линейного программирования

Ниже приводится естественная формулировка задачи линейного программирования для задачи поиска кратчайшего пути. Он очень прост по сравнению с большинством других применений линейных программ в дискретной оптимизации , однако он иллюстрирует связи с другими концепциями.

Дан ориентированный граф ( V , A ) с исходным узлом s , целевым узлом t и стоимостью w _ij для каждого ребра ( i , j ) в A , рассмотрим программу с переменными x _ij

минимизировать при условии и для всех i ,

{\ displaystyle \ sum _ {ij \ in A} w_ {ij} x_ {ij}}

{\ Displaystyle х \ geq 0}

{\ displaystyle \ sum _ {j} x_ {ij} - \ sum _ {j} x_ {ji} = {\ begin {cases} 1, & {\ text {if}} i = s; \\ - 1, & {\ text {if}} i = t; \\ 0, & {\ text {иначе.}} \ end {case}}}

Интуиция за этим заключается в том, что это индикаторная переменная, определяющая , является ли edge ( i , j ) частью кратчайшего пути: 1, если это так, и 0, если это не так. Мы хотим выбрать набор ребер с минимальным весом при условии, что этот набор образует путь от s до t (представленный ограничением равенства: для всех вершин, кроме s и t, количество входящих и исходящих ребер, которые являются частью пути должны быть одинаковыми (т.е. это должен быть путь от s до t). ${\ displaystyle x_ {ij}}$

Этот LP обладает особым свойством - он целостен; более конкретно, каждое базовое оптимальное решение (если оно существует) имеет все переменные, равные 0 или 1, а набор ребер, переменные которых равны 1, образуют s - t- дугу . См. Ahuja et al. для одного доказательства, хотя происхождение этого подхода восходит к середине 20 века.

Дуальный для этой линейной программы

максимизировать y _t - y _s при всех ij , y _j - y _i ≤ w _ij

а возможные двойники соответствуют концепции согласованной эвристики для алгоритма A * для кратчайших путей. Для любой возможной двойной у на снижение затрат неотрицательны и А * в основном работает алгоритм Дейкстры на этих сниженным ценам. ${\ displaystyle w '_ {ij} = w_ {ij} -y_ {j} + y_ {i}}$

Общая алгебраическая структура полуколец: проблема алгебраических путей

Многие проблемы могут быть сформулированы как форма кратчайшего пути для некоторых подходящих понятий сложения вдоль пути и взятия минимума. Общий подход к ним состоит в том, чтобы рассматривать две операции как операции полукольца . Умножение полукольцом выполняется по пути, а сложение - между путями. Эта общая структура известна как проблема алгебраического пути .

Большинство классических алгоритмов поиска кратчайшего пути (и новых) можно сформулировать как решение линейных систем над такими алгебраическими структурами.

Совсем недавно была разработана еще более общая структура для решения этих (и гораздо менее очевидных связанных проблем) под знаменем алгебр оценки .

Кратчайший путь в стохастических сетях, зависящих от времени

В реальных ситуациях транспортная сеть обычно бывает стохастической и зависит от времени. Фактически, путешественник, который ежедневно пересекает ссылку, может испытывать разное время в пути по этой ссылке не только из-за колебаний спроса на поездки (матрица отправления-назначения), но также из-за таких инцидентов, как рабочие зоны, плохие погодные условия, аварии и поломки транспортных средств. . В результате стохастическая зависящая от времени (STD) сеть является более реалистичным представлением реальной дорожной сети по сравнению с детерминированной.

Несмотря на значительный прогресс, достигнутый в течение последнего десятилетия, остается спорным вопрос, как следует определять и идентифицировать оптимальный путь в стохастических дорожных сетях. Другими словами, не существует однозначного определения оптимального пути в условиях неопределенности. Один из возможных и распространенных ответов на этот вопрос - найти путь с минимальным ожидаемым временем в пути. Основное преимущество использования этого подхода состоит в том, что эффективные алгоритмы кратчайшего пути, введенные для детерминированных сетей, могут быть легко использованы для идентификации пути с минимальным ожидаемым временем прохождения в стохастической сети. Однако результирующий оптимальный путь, определенный этим подходом, может быть ненадежным, поскольку этот подход не учитывает изменчивость времени в пути. Чтобы решить эту проблему, некоторые исследователи используют распределение времени в пути вместо его ожидаемого значения, поэтому они находят распределение вероятностей общего времени в пути, используя различные методы оптимизации, такие как динамическое программирование и алгоритм Дейкстры . Эти методы используют стохастическую оптимизацию , в частности стохастическое динамическое программирование, чтобы найти кратчайший путь в сетях с вероятностной длиной дуги. Концепция надежности времени в пути используется взаимозаменяемо с изменчивостью времени в пути в исследовательской литературе по транспорту, так что в целом можно сказать, что чем выше изменчивость времени в пути, тем ниже будет надежность, и наоборот.

Для более точного учета надежности времени в пути были предложены два общих альтернативных определения оптимального пути в условиях неопределенности. Некоторые ввели концепцию наиболее надежного пути, стремясь максимизировать вероятность прибытия вовремя или раньше, чем заданный бюджет времени в пути. Другие, в качестве альтернативы, выдвинули концепцию α-надежного пути, на основе которой они намеревались минимизировать бюджет времени в пути, необходимый для обеспечения заранее заданной вероятности своевременного прибытия.

Смотрите также

Двунаправленный поиск , алгоритм, который находит кратчайший путь между двумя вершинами на ориентированном графе.
Евклидов кратчайший путь
Поточная сеть
Маршрутизация кратчайшего пути K
Умножение матриц мин-плюс
Найти путь
Преодоление кратчайшего пути
Дерево кратчайшего пути

дальнейшее чтение

Frigioni, D .; Marchetti-Spaccamela, A .; Нанни, У. (1998). «Задача кратчайшего пути от одного источника с ограниченным полностью динамическим выходом». Proc. 7-й год. ACM-SIAM Symp. Дискретные алгоритмы . Атланта, Джорджия. С. 212–221. CiteSeerX 10.1.1.32.9856 .
Дрейфус, С.Е. (октябрь 1967 г.). Оценка некоторых алгоритмов кратчайшего пути (PDF) (отчет). Project Rand. ВВС США. РМ-5433-ПР. DTIC AD-661265.

Languages

In other projects