Лемма Спернера - Sperner's lemma
В математике , лемма Шпернера является комбинаторным аналогом из теоремы Брауэра о неподвижной точке , которая является эквивалентной ей.
Лемма состояние Шпернера , что каждые шпернеровы окраски ( как описано ниже) в триангуляции из п - мерного симплекса содержит ячейку окрашенную с полным набором цветов.
Первоначальный результат такого рода был доказан Эмануэлем Спернером в связи с доказательствами инвариантности области . Раскраски Спернера использовались для эффективного вычисления фиксированных точек и в алгоритмах поиска корня , а также в алгоритмах справедливого деления (вырезания торта). В настоящее время считается трудноразрешимой вычислительной задачей найти неподвижную точку Брауэра или, что эквивалентно, раскраску Спернера, даже на плоскости, в общем случае. Проблема заключается в том PPAD-полной , класс сложности изобретен Пападимитриу .
Согласно Советской математической энциклопедии (под ред. И. М. Виноградова ), родственная теорема 1929 г. ( Кнастера , Борсука и Мазуркевича ) также стала известна как лемма Спернера - этот момент обсуждается в английском переводе (под ред. М. Хазевинкеля). Сейчас она широко известна как лемма Кнастера – Куратовского – Мазуркевича .
Заявление
Одномерный случай
В одном измерении лемму Спернера можно рассматривать как дискретную версию теоремы о промежуточном значении . В этом случае, по сути, говорится, что если дискретная функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, то она должна переключать значения нечетное количество раз.
Двумерный случай
Наиболее часто упоминается двумерный случай. Утверждается следующее:
Для треугольника ABC и триангуляции T треугольника множество S вершин графа T раскрашено в три цвета таким образом, что
- A, B и C имеют цвета 1, 2 и 3 соответственно.
- Каждая вершина на ребре ABC должна быть окрашена только в один из двух цветов концов этого ребра. Например, каждая вершина на AC должна иметь цвет 1 или 3.
Тогда существует треугольник из T , вершины которого раскрашены в три разных цвета. Точнее, таких треугольников должно быть нечетное количество.
Многомерный случай
В общем случае лемма относится к n -мерному симплексу
Мы рассматриваем триангуляцию T, которая является непересекающимся делением на меньшие n -мерные симплексы. Обозначим красящего функцию как F : S → {1,2,3, ..., п , п + 1}, где S снова множество вершин Т . Правила раскраски таковы:
- Вершины большого симплекса раскрашены в разные цвета, т. Е. Для .
- Вершины T, расположенные на любой k -мерной подповерхности большого симплекса
- раскрашены только цветами
Тогда существует нечетное количество симплексов из T , вершины которых раскрашены во все n + 1 цвета. В частности, должен быть хотя бы один.
Доказательство
Сначала мы обратимся к двумерному случаю. Рассмотрим граф G, построенный из триангуляции T следующим образом:
- Вершины G - это элементы T плюс площадь вне треугольника. Две вершины соединяются ребром, если их соответствующие области имеют общую границу, причем одна конечная точка окрашена в 1, а другая - в 2.
Обратите внимание, что на интервале AB есть нечетное количество границ, окрашенных в 1-2 (просто потому, что A окрашен в 1, B окрашен в 2; и когда мы движемся по AB, должно быть нечетное количество изменений цвета, чтобы получить разные цвета в начале и в конце). Следовательно, вершина G, соответствующая внешней области, имеет нечетную степень. Но известно ( лемма о рукопожатии ), что в конечном графе есть четное число вершин нечетной степени. Таким образом, оставшийся граф, исключая внешнюю область, имеет нечетное число вершин с нечетной степенью , соответствующими членам T .
Легко видеть, что единственная возможная степень треугольника из T равна 0, 1 или 2, и что степень 1 соответствует треугольнику, раскрашенному тремя цветами 1, 2 и 3.
Таким образом, мы получили немного более сильный вывод, который говорит, что в триангуляции T существует нечетное количество (и по крайней мере один) полноцветных треугольников.
Многомерный случай доказывается индукцией по размерности симплекса. Мы применяем те же рассуждения, что и в двумерном случае, чтобы заключить, что в n- мерной триангуляции существует нечетное число полноцветных симплексов.
Комментарий
Вот уточнение ранее приведенного доказательства для читателя, плохо знакомого с теорией графов .
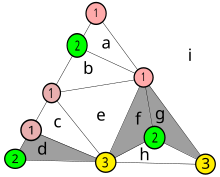
На этой диаграмме нумеруются цвета вершин приведенного ранее примера. Маленькие треугольники, все вершины которых имеют разные номера, на графике заштрихованы. Каждый маленький треугольник становится узлом в новом графе, полученном в результате триангуляции. Маленькие буквы обозначают области, восемь внутри фигуры, а область i обозначает пространство за ее пределами.
Как описано ранее, те узлы, которые имеют общее ребро, конечные точки которого пронумерованы 1 и 2, соединяются в производном графе. Например, узел d имеет общее ребро с внешней областью i , а все его вершины имеют разные номера, поэтому он также закрашен. Узел b не закрашен, потому что две вершины имеют одинаковые номера, но он присоединен к внешней области.
Можно добавить новый треугольник с полным номером, скажем, вставив узел с номером 3 на ребро между 1 и 1 узла a и соединив этот узел с другой вершиной a . Для этого потребуется создать пару новых узлов, как в случае с узлами f и g .
Обобщения
Подмножества этикеток
Предположим, что каждая вершина триангуляции может быть помечена несколькими цветами, так что функция окраски будет f : S → 2 [n + 1] .
Для каждого суб-симплекса набор маркировок на его вершинах является набором-семейством над набором цветов . Это семейство множеств можно рассматривать как гиперграф .
Если для каждой вершины на грани симплекса цвета в являются подмножеством набора цветов на концах грани, то существует под-симплекс со сбалансированной разметкой - разметка, в которой соответствующий гиперграф допускает совершенный дробное соответствие . Чтобы проиллюстрировать это, вот несколько примеров сбалансированной маркировки для :
- ({1}, {2}, {3}) - уравновешиваются весами (1, 1, 1).
- ({1,2}, {2,3}, {3,1}) - уравновешиваются весами (1/2, 1/2, 1/2).
- ({1,2}, {2,3}, {1}) - уравновешивается весами (0, 1, 1).
Это было доказано Шепли в 1973 году. Это комбинаторный аналог леммы KKMS .
Многогранники
Предположим, что вместо -мерного симплекса у нас есть -мерный многогранник с вершинами.
Тогда есть по крайней мере полностью помеченные симплексы, где «полностью помечены» означает, что каждая метка на симплексе имеет свой цвет. Например, если (двумерный) многоугольник с n вершинами триангулирован и раскрашен в соответствии с критерием Спернера, то есть по крайней мере полностью помеченные треугольники.
Это общее утверждение было выдвинуто Атанасовым в 1996 году, который доказал его на практике . Доказательство общего случая было впервые дано де Лоэрой, Петерсоном и Су в 2002 году.
Вариант радуги
Предположим, что вместо одной разметки у нас есть разные разметки Спернера.
Мы рассматриваем пары (симплекс, перестановка) такие, что метка каждой вершины симплекса выбирается из разных разметок (так что для каждого симплекса существуют разные пары).
Тогда есть по крайней мере полностью помеченные пары. Это доказал Равиндра Бапат .
Другой способ сформулировать эту лемму состоит в следующем. Предположим, что есть люди, каждый из которых производит разные разметки Спернера для одной и той же триангуляции. Тогда существует симплекс и соответствие людей его вершинам, так что каждая вершина помечена своим владельцем по-разному (один человек маркирует свою вершину цифрой 1, другой человек маркирует ее вершину цифрой 2 и т. Д.). Более того, таких совпадений не меньше . Это может быть использовано, чтобы найти нарезку для торта без зависти с соединенными кусочками.
Множественные надписи
Предположим, что вместо одной разметки у нас есть разные разметки Спернера. Потом:
- Для любых положительных целых чисел , сумма которых равна , существует детский симплекс, на котором для каждого числа разметки используются по крайней мере (из ) различные метки. Причем каждая метка используется как минимум в одной (вне ) маркировке.
- Для любых положительных целых чисел , сумма которых равна , существует детский симплекс, на котором для каждого метка используется по крайней мере (из ) различных разметок.
Обе версии сводятся к лемме Спернера, когда или когда все разметки идентичны.
См. Аналогичные обобщения.
Градусы
| Последовательность | Степень |
|---|---|
| 123 | 1 (один переключатель 1-2 и нет переключателя 2-1) |
| 12321 | 0 (один переключатель 1-2 минус один переключатель 2-1) |
| 1232 | 0 (как указано выше; последовательность отзыва циклическая) |
| 1231231 | 2 (два переключателя 1-2 и нет переключателя 2-1) |
Предположим, что треугольник триангулирован и помечен {1,2,3}. Рассмотрим циклическую последовательность меток на границе треугольника. Определите степень маркировки как разницу между количеством переключателей от 1 до 2 и количеством переключателей от 2 до 1. См. Примеры в таблице справа. Обратите внимание, что степень одинакова, если мы считаем переключатели от 2 до 3 минус 3 до 2 или от 3 до 1 минус 1 до 3.
Мусин доказал, что количество полностью помеченных треугольников не меньше степени маркировки . В частности, если степень отлична от нуля, то существует хотя бы один полностью помеченный треугольник.
Если разметка удовлетворяет условию Спернера, то ее степень равна 1: переключатели 1-2 и 2-1 находятся только на стороне между вершинами 1 и 2, а количество переключателей 1-2 должно быть на единицу больше, чем число 2–1 переключений (при переходе от вершины 1 к вершине 2). Следовательно, первоначальная лемма Шпернера следует из теоремы Мусина.
Деревья и циклы
Аналогичная лемма есть о конечных и бесконечных деревьях и циклах .
Кубическая лемма Шпернера
Вариант леммы Спернера о кубе (вместо симплекса) был доказан Гарольдом В. Куном . Это связано с теоремой Пуанкаре – Миранды .
Приложения
Раскраски Спернера использовались для эффективного вычисления фиксированных точек . Раскраска Спернера может быть построена так, что полностью помеченные симплексы соответствуют неподвижным точкам данной функции. Делая триангуляцию все меньше и меньше, можно показать, что предел полностью помеченных симплексов - это в точности фиксированная точка. Следовательно, этот метод позволяет приблизить фиксированные точки.
По этой причине, лемма Шпернера также может быть использована в алгоритмах корневых ознакомительный и справедливое разделение алгоритмах; см. протоколы Симмонса – Су .
Лемма Спернера - один из ключевых ингредиентов доказательства теоремы Монски о том , что квадрат нельзя разрезать на нечетное количество треугольников равной площади .
Лемму Спернера можно использовать для поиска конкурентного равновесия в экономике обмена , хотя есть более эффективные способы его найти.
Спустя пятьдесят лет после первой публикации Спернер представил обзор развития, влияния и применения своей комбинаторной леммы.
Эквивалентные результаты
Существует несколько теорем о неподвижной точке, которые представлены в трех эквивалентных вариантах: вариант алгебраической топологии , комбинаторный вариант и вариант покрытия множества. Каждый вариант можно доказать отдельно, используя совершенно разные аргументы, но каждый вариант также можно свести к другим вариантам в своем ряду. Кроме того, каждый результат в верхней строке можно вывести из результата, находящегося под ним в том же столбце.
| Алгебраическая топология | Комбинаторика | Установить покрытие |
|---|---|---|
| Теорема Брауэра о неподвижной точке | Лемма Спернера | Лемма Кнастера – Куратовского – Мазуркевича. |
| Теорема Борсука – Улама. | Лемма Такера | Теорема Люстерника – Шнирельмана. |
Смотрите также
использованная литература
внешние ссылки
- Доказательство леммы Шпернера в вырезе на-узле
- Лемма Спернера и игра треугольников на n-богатом сайте.
- Лемма Спернера в 2D , веб-игра на itch.io.










![{\ Displaystyle [п + 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e000e2c0c8f32b2615e0bf624fdd22e7d93efb)




















