Уравнение импульса Коши - Cauchy momentum equation

Уравнение импульса Коши - это векторное уравнение в частных производных , предложенное Коши, которое описывает нерелятивистский перенос импульса в любом континууме .

Основное уравнение

В конвективной (или лагранжевой ) форме уравнение импульса Коши записывается как:

${\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}$

куда

• ${\ displaystyle \ mathbf {u}}$является скорость потока векторного поля, которое зависит от времени и пространства, (единица измерения: )${\ Displaystyle \ mathrm {м / с}}$
• ${\ displaystyle t}$это время , (единица измерения: )${\ Displaystyle \ mathrm {s}}$
• ${\ displaystyle {\ frac {D \ mathbf {u}} {Dt}}}$является производной материал из , равного , (единицы измерения: )${\ displaystyle \ mathbf {u}}$${\ displaystyle \ partial _ {t} \ mathbf {u} + \ mathbf {u} \ cdot \ nabla \ mathbf {u}}$${\ Displaystyle \ mathrm {м / с ^ {2}}}$
• ${\ displaystyle \ rho}$это плотность в данной точке континуума (для которого уравнение непрерывности имеет место), (единица измерения: )${\ displaystyle \ mathrm {кг / м ^ {3}}}$
• ${\ displaystyle {\ boldsymbol {\ sigma}}}$есть тензор напряжения , (единица измерения: )${\ Displaystyle \ mathrm {Па = Н / м ^ {2} = кг \ cdot m ^ {- 1} \ cdot s ^ {- 2}}}$
• ${\ displaystyle \ mathbf {f} = {\ begin {bmatrix} f_ {x} \\ f_ {y} \\ f_ {z} \ end {bmatrix}}}$представляет собой вектор , содержащий все ускорений , вызванных силами тела (иногда просто гравитационное ускорение ), (единица измерения: )${\ Displaystyle \ mathrm {м / с ^ {2}}}$
• ${\ displaystyle \ nabla \ cdot {\ boldsymbol {\ sigma}} = {\ begin {bmatrix} {\ dfrac {\ partial \ sigma _ {xx}} {\ partial x}} + {\ dfrac {\ partial \ sigma _ {yx}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zx}} {\ partial z}} \\ {\ dfrac {\ partial \ sigma _ {xy}} {\ partial x }} + {\ dfrac {\ partial \ sigma _ {yy}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zy}} {\ partial z}} \\ {\ dfrac {\ partial \ sigma _ {xz}} {\ partial x}} + {\ dfrac {\ partial \ sigma _ {yz}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zz}} {\ partial z}} \\\ конец {bmatrix}}}$- расходимость тензора напряжений. (единица измерения: )${\ displaystyle \ mathrm {Па / м = кг \ cdot m ^ {- 2} \ cdot s ^ {- 2}}}$

Обратите внимание, что для ясности мы используем только векторы-столбцы (в декартовой системе координат ) выше, но уравнение записывается с использованием физических компонентов (которые не являются ни ковариантами («столбец»), ни контрвариантами («строка»)). Однако, если мы выбрали неортогональную криволинейную систему координат , тогда мы должны вычислять и записывать уравнения в ковариантной («векторы-строки») или контравариантной («векторы-столбцы») форме.

После соответствующей замены переменных его также можно записать в форме сохранения :

${\ displaystyle {\ frac {\ partial \ mathbf {j}} {\ partial t}} + \ набла \ cdot \ mathbf {F} = \ mathbf {s}}$

где j - плотность импульса в данной точке пространства-времени, F - поток, связанный с плотностью импульса, а s содержит все объемные силы на единицу объема.

Дифференциальный вывод

Начнем с обобщенного принципа сохранения импульса, который можно записать следующим образом: «Изменение импульса системы пропорционально результирующей силе, действующей на эту систему». Это выражается формулой:

${\ displaystyle {\ vec {p}} (t + \ Delta t) - {\ vec {p}} (t) = \ Delta t {\ vec {\ bar {F}}}}$

где - импульс во времени t , - усредненная сила . После деления на и перехода к пределу получаем ( производная ): ${\ Displaystyle {\ vec {p}} (т)}$${\ displaystyle {\ vec {\ bar {F}}}}$${\ displaystyle \ Delta t}$${\ displaystyle \ Delta t}$${\ displaystyle \ Delta t \ to 0}$

${\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ vec {F}}}$

Давайте проанализируем каждую сторону приведенного выше уравнения.

Правая сторона

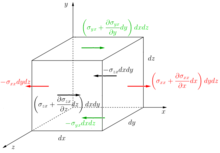
Компонент X сил, действующих на стенки кубического жидкого элемента (зеленый для верхних и нижних стенок; красный для левых и правых; черный для передних и задних).

На верхнем графике мы видим аппроксимацию функции (синяя линия) с использованием конечной разности (желтая линия). На нижнем графике мы видим «бесконечно увеличенную окрестность точки » (фиолетовый квадрат на верхнем графике). На нижнем графике желтая линия полностью закрыта синей и поэтому не видна. На нижнем рисунке использованы две эквивалентные производные формы: ] и обозначение .${\ displaystyle f (x)}$${\ displaystyle x_ {1}}$${\ textstyle f '(x_ {1}) = {\ frac {df (x_ {1})} {dx_ {1}}}}$${\ Displaystyle \ Delta f = f (x_ {1} + \ Delta x) -f (x_ {1})}$

Мы разделяем силы на телесные и поверхностные.${\ displaystyle {\ vec {F}} _ {m}}$ ${\ displaystyle {\ vec {F}} _ {p}}$

${\ displaystyle {\ vec {F}} = {\ vec {F}} _ {p} + {\ vec {F}} _ {m}}$

Поверхностные силы действуют на стенки кубического жидкостного элемента. Для каждой стены компонент X этих сил был отмечен на рисунке кубическим элементом (в виде произведения напряжения и площади поверхности, например, единиц ). ${\ displaystyle - \ sigma _ {xx} \, dy \, dz}$${\ textstyle \ mathrm {Pa \ cdot m \ cdot m = {\ frac {N} {m ^ {2}}} \ cdot m ^ {2} = N}}$

Объяснение значения сил (приближения и минус), действующих на стенки куба.

Это требует некоторого объяснения, почему напряжение, приложенное к стенам, покрывающим оси координат, принимает знак минус (например, для левой стены у нас есть ). Для простоты остановимся на левой стене с натяжением . Знак минус связан с тем, что вектор, нормальный к этой стене, является отрицательным единичным вектором. Затем мы вычислили вектор напряжений по определению , таким образом, компонент X этого вектора (мы используем аналогичные рассуждения для напряжений, действующих на нижнюю и заднюю стенки, то есть:) . ${\ displaystyle - \ sigma _ {xx}}$${\ displaystyle - \ sigma _ {xx}}$${\ displaystyle {\ vec {n}} = [- 1,0,0] = - {\ vec {e}} _ {x}}$${\ displaystyle {\ vec {s}} = {\ vec {n}} \ cdot {\ boldsymbol {\ sigma}} = [- \ sigma _ {xx}, - \ sigma _ {xy}, - \ sigma _ {xz}]}$${\ displaystyle s_ {x} = - \ sigma _ {xx}}$${\ displaystyle - \ sigma _ {yx}, - \ sigma _ {zx}}$ Второй элемент, требующий пояснения, - это аппроксимация значений напряжений, действующих на стенки напротив стен, охватывающих оси. Обратим внимание на правую стенку, где напряжение является приближением напряжения от левой стенки в точках с координатами, и оно равно . Это приближение является результатом применения формулы Тейлора для аппроксимации функции, т.е. ${\ displaystyle \ sigma _ {xx}}$${\ displaystyle x + dx}$${\ displaystyle \ sigma _ {xx} + {\ frac {\ partial \ sigma _ {xx}} {\ partial x}} dx}$ ${\ displaystyle \ sigma _ {xx} (x + dx) = \ sigma _ {xx} (x) + dx {\ frac {\ partial \ sigma _ {xx} (x)} {\ partial x}} + { \ frac {dx ^ {2}} {2}} {\ frac {\ partial ^ {2} \ sigma _ {xx} (x)} {\ partial x ^ {2}}} + \ cdots}$ Поскольку значение бесконечно меньше, чем значение , все компоненты с мощностью больше единицы могут быть пропущены как несущественные. Таким образом, мы получили искомую аппроксимацию натяжения на противоположной стене. Более интуитивное представление значения точки аппроксимации показано на рисунке под кубом. Мы продолжаем аналогичные рассуждения для аппроксимации напряжений . ${\ displaystyle dx ^ {2}}$${\ displaystyle dx}$${\ displaystyle dx}$${\ displaystyle \ sigma _ {xx}}$${\ displaystyle x + dx}$${\ displaystyle \ sigma _ {yx}, \ sigma _ {zx}}$

Складывая силы (их X- компоненты), действующие на каждую из стенок куба, получаем:

${\ Displaystyle F_ {p} ^ {x} = \ left (\ sigma _ {xx} + {\ frac {\ partial \ sigma _ {xx}} {\ partial x}} dx \ right) dy \, dz- \ sigma _ {xx} dy \, dz + \ left (\ sigma _ {yx} + {\ frac {\ partial \ sigma _ {yx}} {\ partial y}} dy \ right) dx \, dz- \ sigma _ {yx} dx \, dz + \ left (\ sigma _ {zx} + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}} dz \ right) dx \, dy- \ sigma _ { zx} dx \, dy}$

После заказа и выполнения аналогичных рассуждений для компонентов (они не показаны на рисунке, но это будут векторы, параллельные осям Y и Z соответственно), мы получим: ${\ Displaystyle F_ {p} ^ {x}}$${\ Displaystyle F_ {p} ^ {y}, F_ {p} ^ {z}}$

${\ displaystyle F_ {p} ^ {x} = {\ frac {\ partial \ sigma _ {xx}} {\ partial x}} \, dx \, dy \, dz + {\ frac {\ partial \ sigma _ { yx}} {\ partial y}} \, dy \, dx \, dz + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}} \, dz \, dx \, dy}$

${\ Displaystyle F_ {p} ^ {y} = {\ frac {\ partial \ sigma _ {xy}} {\ partial x}} \, dx \, dy \, dz + {\ frac {\ partial \ sigma _ { yy}} {\ partial y}} \, dy \, dx \, dz + {\ frac {\ partial \ sigma _ {zy}} {\ partial z}} \, dz \, dx \, dy}$

${\ Displaystyle F_ {p} ^ {z} = {\ frac {\ partial \ sigma _ {xz}} {\ partial x}} \, dx \, dy \, dz + {\ frac {\ partial \ sigma _ { yz}} {\ partial y}} \, dy \, dx \, dz + {\ frac {\ partial \ sigma _ {zz}} {\ partial z}} \, dz \, dx \, dy}$

Затем мы можем записать это в символической операционной форме:

${\ displaystyle {\ vec {F}} _ {p} = (\ nabla \ cdot {\ boldsymbol {\ sigma}}) \, dx \, dy \, dz}$

Внутри контрольного объема действуют массовые силы. Мы можем записать их, используя поле ускорения (например, ускорение свободного падения): ${\ displaystyle \ mathbf {f}}$

${\ displaystyle {\ vec {F}} _ {m} = \ mathbf {f} \ rho \, dx \, dy \, dz}$

Левая сторона

Вычислим импульс куба:

${\ Displaystyle {\ vec {p}} = \ mathbf {u} m = \ mathbf {u} \ rho \, dx \, dy \, dz}$

Поскольку мы предполагаем, что проверяемая масса (куб) постоянна во времени, поэтому ${\ Displaystyle м = \ ро \, dx \, dy \, dz}$

${\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ frac {d \ mathbf {u}} {dt}} \ rho \, dx \, dy \, dz}$

Сравнение левой и правой стороны

У нас есть

${\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ vec {F}}}$

тогда

${\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ vec {F}} _ {p} + {\ vec {F}} _ {m}}$

тогда

${\ displaystyle {\ frac {d \ mathbf {u}} {dt}} \ rho \, dx \, dy \, dz = (\ nabla \ cdot {\ boldsymbol {\ sigma}}) dx \, dy \, dz + \ mathbf {f} \ rho \, dx \, dy \, dz}$

Разделим обе стороны на , и потому получим: ${\ Displaystyle \ rho \, dx \, dy \, dz}$${\ textstyle {\ frac {d \ mathbf {u}} {dt}} = {\ frac {D \ mathbf {u}} {Dt}}}$

${\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}$

что завершает вывод.

Интегральный вывод

Применение второго закона Ньютона ( i- го компонента) к контрольному объему в моделируемом континууме дает:

${\ displaystyle ma_ {i} = F_ {i}}$

Тогда, основываясь на транспортной теореме Рейнольдса и используя обозначения материальной производной , можно записать

${\ displaystyle {\ begin {align} \ int _ {\ Omega} \ rho {\ frac {Du_ {i}} {Dt}} \, dV & = \ int _ {\ Omega} \ nabla _ {j} \ sigma _ {i} ^ {j} \, dV + \ int _ {\ Omega} \ rho f_ {i} \, dV \\\ int _ {\ Omega} \ left (\ rho {\ frac {Du_ {i}}) {Dt}} - \ nabla _ {j} \ sigma _ {i} ^ {j} - \ rho f_ {i} \ right) \, dV & = 0 \\\ rho {\ frac {Du_ {i}} { Dt}} - \ nabla _ {j} \ sigma _ {i} ^ {j} - \ rho f_ {i} & = 0 \\ {\ frac {Du_ {i}} {Dt}} - {\ frac { \ nabla _ {j} \ sigma _ {i} ^ {j}} {\ rho}} - f_ {i} & = 0 \ end {выровнено}}}$

где Ω представляет собой контрольный объем. Поскольку это уравнение должно выполняться для любого контрольного объема, должно быть верно, что подынтегральная функция равна нулю, из этого следует уравнение для импульса Коши. Главный шаг (не сделанный выше) при выводе этого уравнения - установить, что производная тензора напряжений является одной из сил, составляющих F _i .

Форма сохранения

Уравнение импульса Коши также можно записать в следующем виде:

просто определив:

${\ displaystyle {\ begin {align} {\ mathbf {j}} & = \ rho \ mathbf {u} \\ {\ mathbf {F}} & = \ rho \ mathbf {u} \ otimes \ mathbf {u} - {\ boldsymbol {\ sigma}} \\ {\ mathbf {s}} & = \ rho \ mathbf {f} \ end {align}}}$

где j - плотность импульса в рассматриваемой точке континуума (для которой выполняется уравнение неразрывности ), F - поток, связанный с плотностью импульса, а s содержит все объемные силы на единицу объема. u ⊗ u - диада скорости.

Здесь j и s имеют такое же количество размерностей N, что и скорость потока и ускорение тела, а F , будучи тензором , имеет N ² .

В формах Эйлера очевидно, что предположение об отсутствии девиаторного напряжения приводит уравнения Коши к уравнениям Эйлера .

Конвективное ускорение

Пример конвективного ускорения. Поток устойчивый (не зависящий от времени), но жидкость замедляется по мере движения вниз по расширяющемуся каналу (предполагая несжимаемый или дозвуковой сжимаемый поток).

Существенной особенностью уравнений Навье – Стокса является наличие конвективного ускорения: эффект не зависящего от времени ускорения потока относительно пространства. Хотя отдельные частицы континуума действительно испытывают зависящее от времени ускорение, конвективное ускорение поля потока является пространственным эффектом, одним из примеров которого является ускорение жидкости в сопле.

Независимо от того, о каком континууме идет речь, конвективное ускорение является нелинейным эффектом. Конвективное ускорение присутствует в большинстве потоков (исключения включают одномерный поток несжимаемой жидкости), но его динамический эффект не учитывается в ползущем потоке (также называемом потоком Стокса). Конвективное ускорение представлено нелинейной величиной u ⋅ ∇ u , которую можно интерпретировать как ( u ⋅ ∇) u или как u ⋅ (∇ u ) , где ∇ u - тензорная производная вектора скорости u . Обе интерпретации дают одинаковый результат.

Оператор адвекции против тензорной производной

Член конвекции можно записать как ( u ⋅ ∇) u , где u ⋅ ∇ - оператор переноса . Это представление можно противопоставить представлению в терминах тензорной производной. Тензорная производная ∇ u - это покомпонентная производная вектора скорости, определяемая как [∇ u ] _mi = ∂ _m v _i , так что ${\ Displaystyle D \ mathbf {u} / Dt}$

${\ displaystyle \ left [\ mathbf {u} \ cdot \ left (\ nabla \ mathbf {u} \ right) \ right] _ {i} = \ sum _ {m} v_ {m} \ partial _ {m} v_ {i} = \ left [(\ mathbf {u} \ cdot \ nabla) \ mathbf {u} \ right] _ {i} \ ,.}$

Форма ягненка

Идентичность векторного исчисления в поперечном произведении ротора выполнена:

${\ Displaystyle \ mathbf {v} \ times \ left (\ nabla \ times \ mathbf {a} \ right) = \ nabla _ {a} \ left (\ mathbf {v} \ cdot \ mathbf {a} \ right) - \ mathbf {v} \ cdot \ nabla \ mathbf {a}}$

где используется индекс Фейнмана ∇ _a , что означает, что градиент с индексом действует только на множитель a .

Лэмб в своей знаменитой классической книге «Гидродинамика» (1895) использовал это тождество, чтобы изменить конвективный член скорости потока во вращательной форме, то есть без тензорной производной:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ mathbf {u} = \ nabla \ left ({\ frac {\ | \ mathbf {u} \ | ^ {2}} {2}} \ right) + \ влево (\ nabla \ times \ mathbf {u} \ right) \ times \ mathbf {u}}$

где вектор называется вектором Лэмба . Уравнение импульса Коши принимает следующий вид: ${\ displaystyle \ mathbf {l} = \ left (\ nabla \ times \ mathbf {u} \ right) \ times \ mathbf {u}}$

${\ displaystyle {\ frac {\ partial \ mathbf {u}} {\ partial t}} + {\ frac {1} {2}} \ nabla \ left (u ^ {2} \ right) + (\ nabla \ раз \ mathbf {u}) \ times \ mathbf {u} = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}$

Используя личность:

${\ displaystyle \ nabla \ cdot \ left ({\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} - {\ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho}$

уравнение Коши принимает следующий вид:

${\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) - \ mathbf {f } = {\ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u}) - {\ frac {\ partial \ mathbf {u}} {\ partial t}}}$

Фактически, в случае внешнего консервативного поля , определяя его потенциал φ :

${\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = { \ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u}) - {\ гидроразрыв {\ partial \ mathbf {u}} {\ partial t}}}$

В случае стационарного потока производная скорости потока по времени исчезает, поэтому уравнение количества движения принимает следующий вид:

${\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = { \ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u})}$

А при проецировании уравнения импульса на направление потока, то есть вдоль линии тока , перекрестное произведение исчезает из-за тождества векторного исчисления тройного скалярного произведения :

${\ displaystyle \ mathbf {u} \ cdot \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho }} \ right) = {\ frac {1} {\ rho ^ {2}}} \ mathbf {u} \ cdot ({\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho)}$

Если тензор напряжений изотропен, то входит только давление: (где I - тождественный тензор), и уравнение импульса Эйлера в случае установившейся несжимаемой жидкости принимает вид: ${\ displaystyle {\ boldsymbol {\ sigma}} = - p \ mathbf {I}}$

${\ displaystyle \ mathbf {u} \ cdot \ nabla \ left ({\ frac {1} {2}} u ^ {2} + \ phi + {\ frac {p} {\ rho}} \ right) + { \ гидроразрыва {p} {\ rho ^ {2}}} \ mathbf {u} \ cdot \ nabla \ rho = 0}$

В случае стационарной несжимаемой жидкости массовое уравнение просто:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla \ rho = 0 \ ,,}$

то есть закон сохранения массы для установившегося потока несжимаемой жидкости утверждает, что плотность вдоль линии тока постоянна . Это приводит к значительному упрощению уравнения импульса Эйлера:

${\ displaystyle \ mathbf {u} \ cdot \ nabla \ left ({\ frac {1} {2}} u ^ {2} + \ phi + {\ frac {p} {\ rho}} \ right) = 0 }$

Теперь очевидно удобство определения полного напора для невязкого потока жидкости:

${\ displaystyle b_ {l} \ Equiv {\ frac {1} {2}} u ^ {2} + \ phi + {\ frac {p} {\ rho}} \ ,,}$

Фактически, приведенное выше уравнение можно просто записать как:

${\ Displaystyle \ mathbf {u} \ cdot \ nabla b_ {l} = 0}$

То есть, баланс количества движения для устойчивого невязкого и несжимаемого потока во внешнем консервативном поле утверждает, что полный напор вдоль линии тока постоянен .

Безвихревые потоки

Форма Лэмба также полезна в безвихревом потоке, где ротор скорости (называемый завихренностью ) ω = ∇ × u равен нулю. В этом случае член конвекции в сводится к ${\ Displaystyle D \ mathbf {u} / Dt}$

${\ displaystyle \ mathbf {u} \ cdot \ nabla \ mathbf {u} = \ nabla \ left ({\ frac {\ | \ mathbf {u} \ | ^ {2}} {2}} \ right).}$

Стрессы

Влияние стресса в потоке континуума представлен ∇ р и ∇ ⋅ Т точки; это градиенты поверхностных сил, аналогичные напряжениям в твердом теле. Здесь ∇ p - градиент давления, возникающий из-за изотропной части тензора напряжений Коши . Эта часть определяется нормальными напряжениями, которые возникают почти во всех ситуациях. Анизотропная часть тензора напряжений дает ∇ ⋅ τ , который обычно описывает вязкие силы; для несжимаемого потока это только эффект сдвига. Таким образом, τ - тензор девиаторных напряжений , а тензор напряжений равен:

${\ displaystyle {\ boldsymbol {\ sigma}} = - p \ mathbf {I} + {\ boldsymbol {\ tau}}}$

где I - единичная матрица в рассматриваемом пространстве, а τ - тензор сдвига.

Все нерелятивистские уравнения сохранения импульса, такие как уравнение Навье – Стокса , можно получить, начав с уравнения импульса Коши и задав тензор напряжений через определяющее соотношение . Выражая тензор сдвига через вязкость и скорость жидкости и предполагая постоянные плотность и вязкость, уравнение количества движения Коши приведет к уравнениям Навье – Стокса . Предполагая невязкий поток , уравнения Навье – Стокса могут еще больше упроститься до уравнений Эйлера .

Расходимость тензора напряжений можно записать как

${\ displaystyle \ nabla \ cdot {\ boldsymbol {\ sigma}} = - \ nabla p + \ nabla \ cdot {\ boldsymbol {\ tau}}.}$

Влияние градиента давления на поток заключается в ускорении потока в направлении от высокого давления к низкому давлению.

Как написано в уравнении импульса Коши, члены напряжения p и τ пока неизвестны, поэтому одно это уравнение нельзя использовать для решения задач. Помимо уравнений движения - второго закона Ньютона - необходима силовая модель, связывающая напряжения с движением потока. По этой причине предположения, основанные на естественных наблюдениях, часто применяются для определения напряжений в терминах других переменных потока, таких как скорость и плотность.

Внешние силы

Векторное поле f представляет собой объемные силы на единицу массы. Обычно они состоят только из ускорения свободного падения , но могут включать и другие, например электромагнитные силы. В неинерциальных системах координат могут возникнуть другие «инерционные ускорения», связанные с вращающимися координатами .

Часто эти силы могут быть представлены как градиент некоторой скалярной величины χ , при этом f = χ, и в этом случае они называются консервативными силами . Например, сила тяжести в направлении z представляет собой градиент - ρgz . Поскольку давление от такой гравитации возникает только как градиент, мы можем включить его в член давления как объемную силу h = p - χ . Члены давления и силы в правой части уравнения Навье – Стокса принимают вид

${\ displaystyle - \ nabla p + \ mathbf {f} = - \ nabla p + \ nabla \ chi = - \ nabla \ left (p- \ chi \ right) = - \ nabla h.}$

Также возможно включить внешние воздействия в термин «стресс», а не в термин «сила тела». Это может даже включать антисимметричные напряжения (входные данные углового момента), в отличие от обычно симметричных внутренних вкладов в тензор напряжений. ${\ displaystyle {\ boldsymbol {\ sigma}}}$

Обезразмеривание

Чтобы уравнения были безразмерными, необходимо определить характерную длину r ₀ и характеристическую скорость u ₀ . Их следует выбирать так, чтобы все безразмерные переменные были первого порядка. Таким образом получаются следующие безразмерные переменные:

${\ Displaystyle {\ begin {align} \ rho ^ {*} & \ Equiv {\ frac {\ rho} {\ rho _ {0}}} & u ^ {*} & \ Equiv {\ frac {u} {u_ {0}}} & r ^ {*} & \ Equiv {\ frac {r} {r_ {0}}} & t ^ {*} & \ Equ {\ frac {u_ {0}} {r_ {0}}} t \\ [6pt] \ nabla ^ {*} & \ Equiv r_ {0} \ nabla & \ mathbf {f} ^ {*} & \ Equiv {\ frac {\ mathbf {f}} {f_ {0}} } & p ^ {*} & \ Equiv {\ frac {p} {p_ {0}}} & {\ boldsymbol {\ tau}} ^ {*} & \ Equiv {\ frac {\ boldsymbol {\ tau}} { \ тау _ {0}}} \ конец {выровнено}}}$

Подстановка этих перевернутых соотношений в уравнения импульса Эйлера дает:

${\ displaystyle {\ frac {\ rho _ {0} u_ {0} ^ {2}} {r_ {0}}} {\ frac {\ partial \ rho ^ {*} \ mathbf {u} ^ {*} } {\ partial t ^ {*}}} + {\ frac {\ nabla ^ {*}} {r_ {0}}} \ cdot \ left (\ rho _ {0} u_ {0} ^ {2} \ rho ^ {*} \ mathbf {u} ^ {*} \ otimes \ mathbf {u} ^ {*} + p_ {0} p ^ {*} \ right) = - {\ frac {\ tau _ {0} } {r_ {0}}} \ nabla ^ {*} \ cdot {\ boldsymbol {\ tau}} ^ {*} + f_ {0} \ mathbf {f} ^ {*}}$

и разделив на первый коэффициент:

${\ displaystyle {\ frac {\ partial \ mathbf {\ rho} ^ {*} u ^ {*}} {\ partial t ^ {*}}} + \ nabla ^ {*} \ cdot \ left (\ rho ^ {*} \ mathbf {u} ^ {*} \ otimes \ mathbf {u} ^ {*} + {\ frac {p_ {0}} {\ rho _ {0} u_ {0} ^ {2}}} p ^ {*} \ right) = - {\ frac {\ tau _ {0}} {\ rho _ {0} u_ {0} ^ {2}}} \ nabla ^ {*} \ cdot {\ boldsymbol { \ tau}} ^ {*} + {\ frac {f_ {0} r_ {0}} {u_ {0} ^ {2}}} \ mathbf {f} ^ {*}}$

Теперь определяем число Фруда :

${\ displaystyle \ mathrm {Fr} = {\ frac {u_ {0} ^ {2}} {f_ {0} r_ {0}}},}$

число Эйлера :

${\ displaystyle \ mathrm {Eu} = {\ frac {p_ {0}} {\ rho _ {0} u_ {0} ^ {2}}},}$

и коэффициент поверхностного трения или тот, который обычно называют коэффициентом лобового сопротивления в области аэродинамики:

${\ displaystyle C _ {\ mathrm {f}} = {\ frac {2 \ tau _ {0}} {\ rho _ {0} u_ {0} ^ {2}}},}$

пропускание соответственно к консервативному переменным , т.е. плотности импульса и плотности силы :

${\ Displaystyle {\ begin {выровнено} \ mathbf {j} & = \ rho \ mathbf {u} \\\ mathbf {g} & = \ rho \ mathbf {f} \ end {align}}}$

окончательно формулируются уравнения (теперь без индексов):

Уравнения Коши в пределе Фруда Fr → ∞ (соответствующие пренебрежимо малому внешнему полю) называются свободными уравнениями Коши:

и в конечном итоге могут быть уравнениями сохранения . Таким образом, предел больших чисел Фруда (низкое внешнее поле) примечателен для таких уравнений и изучается с помощью теории возмущений .

Наконец, в конвективной форме уравнения следующие:

Явные трехмерные конвективные формы

Декартовы трехмерные координаты

Для асимметричных тензоров напряжений уравнения в общем имеют следующий вид:

${\ displaystyle {\ begin {align} x &: & {\ frac {\ partial u_ {x}} {\ partial t}} + u_ {x} {\ frac {\ partial u_ {x}} {\ partial x} } + u_ {y} {\ frac {\ partial u_ {x}} {\ partial y}} + u_ {z} {\ frac {\ partial u_ {x}} {\ partial z}} & = {\ frac {1} {\ rho}} \ left ({\ frac {\ partial \ sigma _ {xx}} {\ partial x}} + {\ frac {\ partial \ sigma _ {yx}} {\ partial y}} + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}} \ right) + f_ {x} \\ [8pt] y &: & {\ frac {\ partial u_ {y}} {\ partial t}} + u_ {x} {\ frac {\ partial u_ {y}} {\ partial x}} + u_ {y} {\ frac {\ partial u_ {y}} {\ partial y}} + u_ { z} {\ frac {\ partial u_ {y}} {\ partial z}} & = {\ frac {1} {\ rho}} \ left ({\ frac {\ partial \ sigma _ {xy}} {\ partial x}} + {\ frac {\ partial \ sigma _ {yy}} {\ partial y}} + {\ frac {\ partial \ sigma _ {zy}} {\ partial z}} \ right) + f_ { y} \\ [8pt] z &: & {\ frac {\ partial u_ {z}} {\ partial t}} + u_ {x} {\ frac {\ partial u_ {z}} {\ partial x}} + u_ {y} {\ frac {\ partial u_ {z}} {\ partial y}} + u_ {z} {\ frac {\ partial u_ {z}} {\ partial z}} & = {\ frac {1 } {\ rho}} \ left ({\ frac {\ partial \ sigma _ {xz}} {\ partial x}} + {\ frac {\ partial \ sigma _ {yz}} {\ partial y}} + { \ f rac {\ partial \ sigma _ {zz}} {\ partial z}} \ right) + f_ {z} \ end {align}}}$

Цилиндрические 3D координаты

Ниже мы запишем основное уравнение в форме тау-давление в предположении, что тензор напряжений симметричен ( ): ${\ Displaystyle \ sigma _ {ij} = \ sigma _ {ji} \ Longrightarrow \ tau _ {ij} = \ tau _ {ji}}$

${\ displaystyle {\ begin {align} r &: & {\ frac {\ partial u_ {r}} {\ partial t}} + u_ {r} {\ frac {\ partial u_ {r}} {\ partial r} } + {\ frac {u _ {\ phi}} {r}} {\ frac {\ partial u_ {r}} {\ partial \ phi}} + u_ {z} {\ frac {\ partial u_ {r}} {\ partial z}} - {\ frac {u _ {\ phi} ^ {2}} {r}} & = - {\ frac {1} {\ rho}} {\ frac {\ partial P} {\ partial r}} + {\ frac {1} {r \ rho}} {\ frac {\ partial \ left (r \ tau _ {rr} \ right)} {\ partial r}} + {\ frac {1} { r \ rho}} {\ frac {\ partial \ tau _ {\ phi r}} {\ partial \ phi}} + {\ frac {1} {\ rho}} {\ frac {\ partial \ tau _ {zr }} {\ partial z}} - {\ frac {\ tau _ {\ phi \ phi}} {r \ rho}} + f_ {r} \\ [8pt] \ phi &: & {\ frac {\ partial u _ {\ phi}} {\ partial t}} + u_ {r} {\ frac {\ partial u _ {\ phi}} {\ partial r}} + {\ frac {u _ {\ phi}} {r}} {\ frac {\ partial u _ {\ phi}} {\ partial \ phi}} + u_ {z} {\ frac {\ partial u _ {\ phi}} {\ partial z}} + {\ frac {u_ {r } u _ {\ phi}} {r}} & = - {\ frac {1} {r \ rho}} {\ frac {\ partial P} {\ partial \ phi}} + {\ frac {1} {r \ rho}} {\ frac {\ partial \ tau _ {\ phi \ phi}} {\ partial \ phi}} + {\ frac {1} {r ^ {2} \ rho}} {\ frac {\ partial \ left (r ^ {2} \ tau _ {r \ phi} \ right)} {\ partia lr}} + {\ frac {1} {\ rho}} {\ frac {\ partial \ tau _ {z \ phi}} {\ partial z}} + f _ {\ phi} \\ [8pt] z &: & {\ frac {\ partial u_ {z}} {\ partial t}} + u_ {r} {\ frac {\ partial u_ {z}} {\ partial r}} + {\ frac {u _ {\ phi}} {r}} {\ frac {\ partial u_ {z}} {\ partial \ phi}} + u_ {z} {\ frac {\ partial u_ {z}} {\ partial z}} & = - {\ frac {1} {\ rho}} {\ frac {\ partial P} {\ partial z}} + {\ frac {1} {\ rho}} {\ frac {\ partial \ tau _ {zz}} {\ partial z}} + {\ frac {1} {r \ rho}} {\ frac {\ partial \ tau _ {\ phi z}} {\ partial \ phi}} + {\ frac {1} {r \ rho} } {\ frac {\ partial \ left (r \ tau _ {rz} \ right)} {\ partial r}} + f_ {z} \ end {align}}}$

Смотрите также

• Уравнения Эйлера (гидродинамика)
• Уравнения Навье – Стокса
• Уравнения Бернетта
• Расширение Чепмена – Энскога

Примечания

использованная литература