Соты кубические усеченные - Bitruncated cubic honeycomb

Усеченные кубические соты

Тип	Равномерные соты
Символ Шлефли	2т {4,3,4} т _1,2 {4,3,4}
Диаграмма Кокстера-Дынкина
Тип ячейки	( 4.6.6 )
Типы лица	квадрат {4} шестиугольник {6}
Край фигура	равнобедренный треугольник {3}
Фигура вершины	( тетрагональный дисфеноид )
Пространственная группа Обозначение фибрифолд Обозначение Кокстера	Im 3 м (229) 8 ^o : 2 [[4,3,4]]
Группа Коксетера	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]
Двойной	Сплюснутые тетраэдры. Дисфеноидные тетраэдрические соты. Ячейка:
Характеристики	изогональный , изотоксальный , изохорный

Усеченные кубические соты, показанные здесь, по отношению к кубическим сотам.

Bitruncated кубического сот представляет собой пространство заполнения тесселяции (или сотни ) в евклидове пространства 3 из усеченных октаэдров (или, что эквивалентно, bitruncated кубов). Он имеет 4 усеченных октаэдра вокруг каждой вершины. Он полностью состоит из усеченных октаэдров и является клеточно-транзитивным . Он также является реберно-транзитивным , с двумя шестиугольниками и одним квадратом на каждом ребре, и вершинно-транзитивным . Это один из 28 однородных сот .

Джон Хортон Конвей называет эти соты усеченными октаэдрилами в своем списке архитектурной и катоптрической мозаики с двойным, называемым сплюснутой тетраэдрилью , также называемой дифеноидными тетраэдрическими сотами . Хотя обычный тетраэдр не может замощить пространство в одиночку, у этого двойника есть идентичные ячейки тетраэдра дисфеноида с гранями равнобедренного треугольника .

Геометрия

Она может быть реализована как Вороная тесселяция из кубической объемно-центрированной решетки. Лорд Кельвин предположил, что оптимальной пеной для мыльных пузырей является вариант кубических сот (с изогнутыми гранями и краями, но с той же комбинаторной структурой). Однако структура Вира – Фелана представляет собой менее симметричную, но более эффективную пену из мыльных пузырей.

Соты представляют собой мозаику пермутоэдра для 3-х пространств. Координаты вершин одного октаэдра представляют собой гиперплоскость целых чисел в 4-м пространстве, в частности перестановки (1,2,3,4). Тесселяция формируется переведенными копиями внутри гиперплоскости.

Тесселяция - это самая высокая мозаика параллелоэдров в 3-м пространстве.

Прогнозы

Bitruncated кубических сота может быть ортогонально проецируется в евклидовой плоскости с различными механизмов симметрии. Форма высшей (гексагональной) симметрии проектируется в неоднородный ромбитрихексагональный мозаичный слой . Проекция квадратной симметрии образует две перекрывающиеся усеченные квадратные плитки , которые объединяются в квадратную плитку со скошенной фаской .

Ортогональные проекции
Симметрия	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Твердый
Рамка

Симметрия

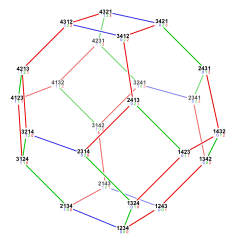
Вершина этой соты представляет собой дисфеноидный тетраэдр , а также тетраэдр Гурса ( фундаментальная область ) для группы Кокстера . Эта сотовая структура имеет четыре одинаковых конструкции, с усеченными октаэдрическими ячейками, имеющими разные группы Кокстера и конструкции Витхоффа . Эти однородные симметрии можно представить, раскрасив по-разному ячейки в каждой конструкции. ${\ displaystyle {\ tilde {A}} _ {3}}$

Пять равномерных раскрасок по ячейкам
Космическая группа	Я 3 мес. (229)	PM 3 мес. (221)	FM 3 м (225)	Ж 4 3 мес. (216)	Fd 3 м (227)
Фибрифолд	8 ^часов : 2	4 ^- : 2	2 ^- : 2	1 ^о : 2	2 ⁺ : 2
Группа Коксетера	${\ displaystyle {\ tilde {C}} _ {3}}$ × 2 [[4,3,4]] = [4 [3 ^[4] ]] знак равно	${\ displaystyle {\ tilde {C}} _ {3}}$ [4,3,4] = [2 [3 ^[4] ]] знак равно	${\ displaystyle {\ tilde {B}} _ {3}}$ [4,3 ^1,1 ] = <[3 ^[4] ]> знак равно	${\ displaystyle {\ tilde {A}} _ {3}}$ [3 ^[4] ]	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 [[3 ^[4] ]] = [[3 ^[4] ]]
Диаграмма Кокстера
усеченные октаэдры	1	1: 1 :	2: 1: 1 : :	1: 1: 1: 1 : : :	1: 1 :
Фигура вершины
Симметрия вершинной фигуры	[2 ⁺ , 4] (заказ 8)	[2] (порядок 4)	[] (порядок 2)	[] ⁺ (заказ 1)	[2] ⁺ (заказ 2)
Изображение, раскрашенное ячейкой

Связанные многогранники и соты

Регулярный перекос apeirohedron {6,4 | 4} содержит шестиугольники этой соты.

[4,3,4], , Группа Кокстера генерирует 15 перестановок однородных мозаик, 9 с отличной геометрией, включая чередующиеся кубические соты. Расширено кубические сотни (также известные как runcinated tesseractic сотни) геометрически идентичны кубические сотни.

C3 соты
Космическая группа	Фибрифолд	Расширенная симметрия	Расширенная диаграмма	порядок	Соты
Рт 3 м (221)	4 ^- : 2	[4,3,4]		× 1	₁ , ₂ , ₃ , ₄ , ₅ , ₆
FM 3 м (225)	2 ^- : 2	[1 ⁺ , 4,3,4] ↔ [4,3 ^1,1 ]	↔	Половина	₇ , ₁₁ , ₁₂ , ₁₃
Я 4 3 мес. (217)	4 ^ч : 2	[[(4,3,4,2 ⁺ )]]		Половина × 2	₍₇₎ ,
Fd 3 м (227)	2 ⁺ : 2	[[1 ⁺ , 4,3,4,1 ⁺ ]] ↔ [[3 ^[4] ]]	↔	Квартал × 2	₁₀ ,
Я 3 мес. (229)	8 ^часов : 2	[[4,3,4]]		× 2	₍₁₎ , ₈ , ₉

[4,3 ^1,1 ],, Группа Кокстера генерирует 9 перестановок однородных мозаик, 4 с отличной геометрией, включая чередующиеся кубические соты.

В3 соты
Космическая группа	Фибрифолд	Расширенная симметрия	Расширенная диаграмма	порядок	Соты
FM 3 м (225)	2 ^- : 2	[4,3 ^1,1 ] ↔ [4,3,4,1 ⁺ ]	↔	× 1	₁ , ₂ , ₃ , ₄
FM 3 м (225)	2 ^- : 2	<[1 ⁺ , 4,3 ^1,1 ]> ↔ <[3 ^[4] ]>	↔	× 2	₍₁₎ , ₍₃₎
Рт 3 м (221)	4 ^- : 2	<[4,3 ^1,1 ]>		× 2	₅ , ₆ , ₇ , ₍₆₎ , ₉ , ₁₀ , ₁₁

Эти соты - одна из пяти отдельных однородных сот, созданных группой Кокстера . Симметрию можно умножить на симметрию колец в диаграммах Кокстера – Дынкина : ${\ displaystyle {\ tilde {A}} _ {3}}$

Соты формата А3
Космическая группа	Фибрифолд	Квадратная симметрия	Расширенная симметрия	Расширенная диаграмма	Расширенная группа	Сотовые диаграммы
Ж 4 3 мес. (216)	1 ^о : 2	а1	[3 ^[4] ]		${\ displaystyle {\ tilde {A}} _ {3}}$	(Никто)
FM 3 м (225)	2 ^- : 2	d2	<[3 ^[4] ]> ↔ [4,3 ^1,1 ]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 ₁ ↔ ${\ displaystyle {\ tilde {B}} _ {3}}$	₁ , ₂
Fd 3 м (227)	2 ⁺ : 2	g2	[[3 ^[4] ]] или [2 ⁺ [3 ^[4] ]]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 ₂	₃
Рт 3 м (221)	4 ^- : 2	d4	<2 [3 ^[4] ]> ↔ [4,3,4]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 4 ₁ ↔ ${\ displaystyle {\ tilde {C}} _ {3}}$	₄
Я 3 (204)	8 ^−o	r8	[4 [3 ^[4] ]] ⁺ ↔ [[4,3 ⁺ , 4]]	↔	½ × 8 ↔ ½ × 2 ${\ displaystyle {\ tilde {A}} _ {3}}$ ${\ displaystyle {\ tilde {C}} _ {3}}$	_(*)
Я 3 мес. (229)	8 ^часов : 2	r8	[4 [3 ^[4] ]] ↔ [[4,3,4]]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 8 ↔ × 2 ${\ displaystyle {\ tilde {C}} _ {3}}$	₅

Альтернативная форма

Альтернативные усеченные кубические соты
Тип	Выпуклые соты
Символ Шлефли	2s {4,3,4} 2s {4,3 ^1,1 } sr {3 ^[4] }
Диаграммы Кокстера	знак равно знак равно знак равно
Клетки	тетраэдр икосаэдр
Фигура вершины
Группа Коксетера	[[4,3 ⁺ , 4]], ${\ displaystyle {\ tilde {C}} _ {3}}$
Двойной	Сотовая ячейка из десяти бриллиантов :
Характеристики	вершинно-транзитивный

Эти соты можно чередовать , создавая пиритоэдрические икосаэдры из усеченных октаэдров с дисфеноидными тетраэдрическими ячейками, созданными в промежутках. Есть три построения из трех связанных диаграмм Кокстера-Дынкина :, , а также . Они обладают симметрией [4,3 ⁺ , 4], [4, (3 ^1,1 ) ⁺ ] и [3 ^[4] ] ⁺ соответственно. Первую и последнюю симметрию можно удвоить как [[4,3 ⁺ , 4]] и [[3 ^[4] ]] ⁺ .

Двойные соты состоят из ячеек, называемых декаэдрами из десяти бриллиантов .

Пять равномерных раскрасок
Космическая группа	Я 3 (204)	Вечер 3 (200)	FM 3 (202)	Fd 3 (203)	F23 (196)
Фибрифолд	8 ^−o	4 ^-	2 ^-	2 ^{o +}	1 ^o
Группа Коксетера	[[4,3 ⁺ , 4]]	[4,3 ⁺ , 4]	[4, (3 ^1,1 ) ⁺ ]	[[3 ^[4] ]] ⁺	[3 ^[4] ] ⁺
Диаграмма Кокстера
порядок	двойной	полный	половина	четверть двойной	четверть
Изображение раскрашено ячейками

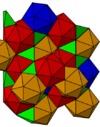
Эти соты представлены атомами бора α-ромбиэдрического кристалла . Центры икосаэдров расположены в ГЦК-позициях решетки.

Связанные многогранники

Неоднородные варианты с симметрией [4,3,4] и двумя типами усеченных октаэдров можно удвоить, поместив два типа усеченных октаэдров, чтобы получить неоднородные соты с усеченными октаэдрами и гексагональными призмами (как дитригональные трапеции). Его вершина представляет собой C _2v -симметричную треугольную бипирамиду .

Затем эти соты можно чередовать, чтобы получить другие неоднородные соты с пиритоэдрическими икосаэдрами , октаэдрами (как треугольные антипризмы) и тетраэдрами (как сфеноиды). Его вершинная фигура имеет симметрию C _2v и состоит из 2 пятиугольников , 4 прямоугольников , 4 равнобедренных треугольников (разделенных на два набора по 2) и 4 равнобедренных треугольников .

Смотрите также

Примечания

использованная литература

Джон Х. Конвей , Хайди Берджел, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 21, Присвоение имен архимедовым и каталонским многогранникам и мозаикам, Архитектурная и катоптрическая мозаика, стр. 292-298, включает все непризматические формы)
Георгий Ольшевский, Uniform Panoploid Tetracombs , Manuscript (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомбов)
Бранко Грюнбаум , Равномерные мозаики трехмерного пространства. Геомбинаторика 4 (1994), 49 - 56.
Калейдоскопы: Избранные сочинения HSM Coxeter , отредактированные Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) HSM Кокстер, Регулярные и полурегулярные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Единообразные заполнители пространств)
А. Андреини , Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и соответствующих коррелятивных сетях), Mem. Итальянское общество науки, сер. 3, 14 (1905) 75–129.
Клитцинг, Ричард. «3D евклидовы соты o4x3x4o - партия - O16» .
Однородные соты в 3-м пространстве: 05-партия
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X.

внешние ссылки

Вайсштейн, Эрик В. "Многогранник, заполняющий пространство" . MathWorld .

Languages

In other projects