Треугольное число в квадрате - Squared triangular number

Квадрат, длина стороны которого равна треугольному числу, можно разделить на квадраты и полуквадраты, площадь которых складывается с кубиками. Из Галлея (2010) .

В теории чисел , сумма первых $п$ кубов есть квадрат из $п$ - го треугольного числа . То есть,

{\ displaystyle 1 ^ {3} + 2 ^ {3} + 3 ^ {3} + \ cdots + n ^ {3} = \ left (1 + 2 + 3 + \ cdots + n \ right) ^ {2} .}

То же уравнение можно записать более компактно, используя математические обозначения для суммирования :

{\ displaystyle \ sum _ {k = 1} ^ {n} k ^ {3} = {\ bigg (} \ sum _ {k = 1} ^ {n} k {\ bigg)} ^ {2}.}

Это тождество иногда называют теоремой Никомаха в честь Никомаха из Герасы (ок. 60 - ок. 120 г. н. Э.).

История

Никомах в конце главы 20 своего Введения в арифметику указал, что если написать список нечетных чисел, первое будет кубом 1, сумма следующих двух будет кубом 2, суммой следующие три - это куб из 3 и так далее. Он не идет дальше этого, но из этого следует, что сумма первых $n$ кубиков равна сумме первых нечетных чисел, то есть нечетных чисел от 1 до . Среднее значение этих чисел очевидно , и их есть , поэтому их сумма равна ${\ Displaystyle п (п + 1) / 2}$ ${\ Displaystyle п (п + 1) -1}$ ${\ Displaystyle п (п + 1) / 2}$ ${\ Displaystyle п (п + 1) / 2}$ ${\ displaystyle {\ bigl (} n (n + 1) / 2 {\ bigr)} ^ {2}.}$

Многие ранние математики изучили и предоставили доказательства теоремы Никомаха. Струкер (1995) утверждает, что «каждый, кто изучает теорию чисел, наверняка восхищался этим чудесным фактом». Пенгелли (2002) находит ссылки на идентичность не только в трудах Никомаха на территории современной Иордании в первом веке нашей эры, но также в работах Арьябхаты в Индии в пятом веке и в трудах Аль-Караджи около 1000 г. Персия . Брессуд (2004) упоминает несколько дополнительных ранних математических работ по этой формуле Аль-Кабиси (Аравия 10 века), Герсонида (около 1300 г., Франция) и Нилакантхи Сомаяджи (около 1500 г., Индия); он воспроизводит визуальное доказательство Нилакантхи.

Числовые значения; геометрическая и вероятностная интерпретация

Все 36 [ (1 + 2 + 3) ² = 1 ³ + 2 ³ + 3 ³ ] прямоугольников, включая 14 [ 1 ² + 2 ² + 3 ² ] квадратов (красные), в квадрате 3 × 3 (4 × 4 вершина) сетка

Последовательность квадратов треугольных чисел:

0, 1, 9, 36, 100, 225,

441, 784, 1296, 2025, 3025, 4356, 6084, 8281,

....

Эти числа можно рассматривать как фигурные числа , четырехмерное гиперпирамидальное обобщение треугольных чисел и квадратных пирамидальных чисел .

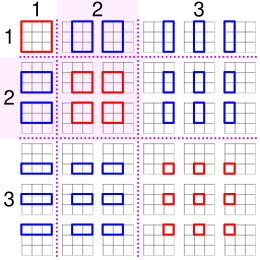
Как отмечает Стейн (1971) , эти числа также подсчитывают количество прямоугольников с горизонтальными и вертикальными сторонами, сформированных в сетке $n \times n$ . Например, точки сетки $4 \times 4$ (или квадрата, состоящего из трех меньших квадратов на стороне) могут образовывать 36 различных прямоугольников. Количество квадратов в квадратной сетке аналогично подсчитывается квадратными пирамидальными числами.

Тождество также допускает естественную вероятностную интерпретацию следующим образом. Пусть $X, Y, Z, W$ - четыре целых числа, независимо и равномерно выбранных случайным образом от $1$ до $n$ . Тогда вероятность того, что $W$ является самым большим из четырех чисел равна вероятности того, что $Y$ является по меньшей мере больше, $X$ и $W$ , по крайней мере , как большой , как $Z$ . То есть . Для любого конкретного значения $W$ комбинации $X$ , $Y$ и $Z,$ которые делают $W$ наибольшим, образуют куб $1 \leq$ $X$ $,$ $Y$ $,$ $Z$ $\leq$ $n,$ поэтому (добавляя размер этого куба ко всем вариантам $W$ ) количество комбинаций из $X$ $,$ $Y$ $,$ $Z$ $,$ $W$ , для которых $W$ является самым большим является суммой кубов, левая часть тождества Nichomachus. Множества пар $($ $X$ $,$ $Y$ $)$ с $X$ $\leq$ $Y$ и пар $($ $Z$ $,$ $W$ $)$ с $Z$ $\leq$ $W$ образуют равнобедренные прямоугольные треугольники, а множество, подсчитываемое в правой части уравнения вероятностей, является декартовым произведением этих два треугольника, поэтому его размер равен квадрату треугольного числа в правой части тождества Нихомаха. Сами вероятности представляют собой соответственно левую и правую части тождества Нихомаха, нормализованные для получения вероятностей путем деления обеих сторон на $n$ $4$ . ${\ Displaystyle P [\ макс (X, Y, Z) \ Leq W] = P [X \ Leq Y \ клин Z \ Leq W]}$

Доказательства

Чарльз Уитстон ( 1854 ) дает особенно простой вывод, расширяя каждый куб в сумме до набора последовательных нечетных чисел. Он начинает с того, что дает личность

{\ displaystyle n ^ {3} = \ underbrace {\ left (n ^ {2} -n + 1 \ right) + \ left (n ^ {2} -n + 1 + 2 \ right) + \ left (n ^ {2} -n + 1 + 4 \ right) + \ cdots + \ left (n ^ {2} + n-1 \ right)} _ {n {\ text {последовательные нечетные числа}}}.}

Эта идентичность связана с треугольными числами следующим образом:

{\ displaystyle T_ {n}}

{\ displaystyle n ^ {3} = \ sum _ {k = T_ {n-1} +1} ^ {T_ {n}} (2k-1),}

и, таким образом, формирование слагаемых начинается сразу после тех, которые формируют все предыдущие значения до . Применение этого свойства вместе с другим хорошо известным идентификатором:

{\ Displaystyle п ^ {3}}

{\ displaystyle 1 ^ {3}}

{\ Displaystyle (п-1) ^ {3}}

{\ displaystyle n ^ {2} = \ sum _ {k = 1} ^ {n} (2k-1),}

производит следующий вывод:

{\ displaystyle {\ begin {align} \ sum _ {k = 1} ^ {n} k ^ {3} & = 1 + 8 + 27 + 64 + \ cdots + n ^ {3} \\ & = \ underbrace {1} _ {1 ^ {3}} + \ underbrace {3 + 5} _ {2 ^ {3}} + \ underbrace {7 + 9 + 11} _ {3 ^ {3}} + \ underbrace {13 + 15 + 17 + 19} _ {4 ^ {3}} + \ cdots + \ underbrace {\ left (n ^ {2} -n + 1 \ right) + \ cdots + \ left (n ^ {2} + n-1 \ right)} _ {n ^ {3}} \\ & = \ underbrace {\ underbrace {\ underbrace {\ underbrace {1} _ {1 ^ {2}} + 3} _ {2 ^ {2 }} + 5} _ {3 ^ {2}} + \ cdots + \ left (n ^ {2} + n-1 \ right)} _ {\ left ({\ frac {n ^ {2} + n} {2}} \ right) ^ {2}} \\ & = (1 + 2 + \ cdots + n) ^ {2} \\ & = {\ bigg (} \ sum _ {k = 1} ^ {n } k {\ bigg)} ^ {2}. \ end {align}}}

Роу (1893) получает другое доказательство, суммируя числа в квадратной таблице умножения двумя разными способами. Сумма- й строки умножается на треугольное число, из которого следует, что сумма всех строк равна квадрату треугольного числа. В качестве альтернативы, можно разложить таблицу на последовательность вложенных гномонов , каждый из которых состоит из продуктов, в которых большее из двух членов является некоторым фиксированным значением. Сумма внутри каждого gmonon - это куб, поэтому сумма всей таблицы - это сумма кубов. ${\ displaystyle i}$ ${\ displaystyle i}$

Наглядная демонстрация того, что квадрат треугольного числа равен сумме кубиков.

В более поздней математической литературе Эдмондс (1957) приводит доказательство с использованием суммирования по частям . Стейн (1971) использует интерпретацию этих чисел как прямоугольник, чтобы сформировать геометрическое доказательство тождества (см. Также Benjamin, Quinn & Wurtz 2006 ); он отмечает, что это можно также легко (но малоинформативно) доказать с помощью индукции, и заявляет, что Теплиц (1963) дает «интересное старое арабское доказательство». Каним (2004) предоставляет чисто визуальное доказательство, Бенджамин и Оррисон (2002) предоставляют два дополнительных доказательства, а Нельсен (1993) дает семь геометрических доказательств.

Обобщения

Аналогичный результат теоремы Никомаха верен для всех степенных сумм , а именно, что нечетные степенные суммы (суммы нечетных степеней) являются многочленами от треугольных чисел. Они называются полиномами Фаульхабера , из которых сумма кубов является самым простым и элегантным примером. Однако ни в каком другом случае сумма одной степени не равна квадрату другой.

Строкер (1995) изучает более общие условия, при которых сумма последовательной последовательности кубов образует квадрат. Гарретт и Хаммел (2004) и Варнаар (2004) изучают полиномиальные аналоги формулы квадратно-треугольного числа, в которой серии многочленов складываются с квадратом другого многочлена.

Примечания

использованная литература

Бенджамин, Артур Т .; Orrison, ME (2002), "Два быстрых комбинаторные доказательства " ${\ displaystyle \ textstyle \ sum k ^ {3} = {n + 1 \ select 2} ^ {2}}$ (PDF) , Колледж Математика Journal , 33 (5): 406-408, DOI : 10,2307 / 1559017 , JSTOR 1559017.
Бенджамин, Артур Т .; Куинн, Дженнифер Дж .; Вюрца, Calyssa (2006), "Суммирование кубов путем подсчета прямоугольников" (PDF) , Колледж Математика Journal , 37 (5): 387-389, DOI : 10,2307 / 27646391 , JSTOR 27646391.
Брессуд, Дэвид (2004), Исчисление до Ньютона и Лейбница, Часть III (PDF) , AP Central.
Эдмондс, Шейла М. (1957), "Суммы степеней натуральных чисел", Математическая газета , 41 : 187-188, DOI : 10,2307 / 3609189 , JSTOR 3609189 , МР 0096615
Гаррет, Кристина С .; Hummel, Кристно (2004), "Комбинаторное доказательство суммы $д$ -куб" , Электронный журнал комбинаторика , 11 (1), научно - исследовательская работа 9, DOI : 10,37236 / 1762 , MR 2034423.
Галли, Нед (4 марта 2010 г.), Шур, Лорен (ред.), Теорема Никомаха , Matlab Central.
Kanim, Кэтрин (2004), "Доказательства без слов: Сумма кубов-расширение суммы Архимеда квадратов", Математика Magazine , 77 (4): 298-299, DOI : 10,2307 / 3219288 , JSTOR 3219288.
Нельсен, Роджер Б. (1993), Доказательства без слов , Cambridge University Press, ISBN 978-0-88385-700-7.
Пенгелли, Дэвид (2002), «Мост между непрерывным и дискретным через оригинальные источники», Study the Masters: The Abel-Fauvel Conference (PDF) , Национальный центр математического образования, Univ. Гётеборг, Швеция.
Роу, Т. Сундара (1893 г.), Геометрические упражнения при складывании бумаги , Мадрас: Аддисон, стр. 47–48..
Stein, Роберт Г. (1971), "Комбинаторное доказательство того, что " Математика Magazine , 44 (3): 161-162, DOI : 10,2307 / 2688231 , JSTOR 2688231 ${\ Displaystyle \ textstyle \ сумма к ^ {3} = (\ сумма к) ^ {2}}$ .
Stroeker, RJ (1995), «О сумме последовательных кубов, составляющих полный квадрат» , Compositio Mathematica , 97 (1-2): 295-307, MR 1355130.
Теплиц, Отто (1963), Исчисление, генетический подход , University of Chicago Press, ISBN 978-0-226-80667-9.
Warnaar, С. Оле (2004), "О $д$ -аналог суммы кубов" , Электронный журнал Комбинаторика , 11 (1), примечание 13, DOI : 10,37236 / 1 854 , МР 2114194.
Уитстона, C. (1854), "О формировании полномочий от арифметической прогрессии" (PDF) , Труды Королевского общества в Лондоне , 7 : 145-151, DOI : 10.1098 / rspl.1854.0036.

Languages

In other projects