Понтрягина двойственность - Pontryagin duality

В математике двойственность Понтрягина - это двойственность между локально компактными абелевыми группами, которая позволяет обобщить преобразование Фурье на все такие группы, которые включают группу окружности (мультипликативная группа комплексных чисел с модулем один), конечные абелевы группы (с дискретной топологией ) , а также аддитивная группа целых чисел (также с дискретной топологией), действительные числа и любое конечномерное векторное пространство над вещественными числами или p -адическим полем .

Понтрягинский двойного локально компактной абелевой группы, является группа , образованная непрерывными гомоморфизмами группы из группы к группе окружности. Теорема двойственности Понтрягина устанавливает двойственность Понтрягина, утверждая, что любая локально компактная абелева группа естественным образом изоморфна своему бидуалу (двойственному к своей двойственной). Теорема обращения Фурье - частный случай этой теоремы.

Тема названа в честь Льва Понтрягина , заложившего основы теории локально компактных абелевых групп и их двойственности во время своих первых математических работ в 1934 году. В трактовке Понтрягина учитывалась счетность второй группы, компактность или дискретность. Это было улучшено Эгбертом ван Кампеном в 1935 году и Андре Вейлем в 1940 году для покрытия общих локально компактных абелевых групп .

Вступление

Двойственность Понтрягина помещает в единый контекст ряд наблюдений о функциях на вещественной прямой или о конечных абелевых группах:

• Подходящие регулярные комплекснозначные периодические функции на вещественной прямой имеют ряды Фурье, и эти функции могут быть восстановлены из их рядов Фурье;
• Подходящие регулярные комплекснозначные функции на вещественной прямой имеют преобразования Фурье, которые также являются функциями на вещественной прямой, и, как и для периодических функций, эти функции могут быть восстановлены из их преобразований Фурье; а также
• Комплекснозначные функции на конечной абелевой группе имеют дискретные преобразования Фурье , которые являются функциями на двойственной группе , которая является (неканонически) изоморфной группой. Более того, любую функцию на конечной абелевой группе можно восстановить с помощью ее дискретного преобразования Фурье.

Теория, введенный Л. С. Понтрягина и в сочетании с мерой Хаара , введенной Джоном фон Нейманом , Вейль и другие , зависит от теории двойственной группы в виде локально компактной абелевой группы.

Это аналогично двойственному векторному пространству векторного пространства: конечномерное векторное пространство V и его двойственное векторное пространство V * естественно не изоморфны, но алгебра эндоморфизмов (матричная алгебра) одного изоморфна противоположному эндоморфизму алгебра другого: через транспонирование. Кроме того , группа и ее двойная группа вообще говоря, не изоморфны, но их кольца эндоморфизмов противоположны друг другу: . Более категорично, это не просто изоморфизм алгебр эндоморфизмов, а контравариантная эквивалентность категорий - см. Категорические соображения . ${\ displaystyle {\ text {End}} (V) \ cong {{\ text {End}} (V ^ {*})} ^ {\ text {op}},}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ text {End}} (G) \ cong {\ text {End}} ({\ widehat {G}}) ^ {\ text {op}}}$

Определение

Топологическая группа является локально компактной группой , если топологическое пространство локально компактно и хаусдорфово ; топологическая группа абелева, если основная группа абелева . Примеры локально компактных абелевых групп включают конечные абелевы группы, целые числа (как для дискретной топологии , которая также индуцируется обычной метрикой), действительные числа, круговую группу T (обе с их обычной метрической топологией), а также p -адические числа (с их обычной p -адической топологией).

Для локально компактной абелевой группы двойственная по Понтрягину группа - это группа непрерывных гомоморфизмов групп из в группу окружности . То есть, ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle T}$

${\ displaystyle {\ widehat {G}}: = \ operatorname {Hom} (G, T).}$

Двойственный по Понтрягину обычно наделен топологией, задаваемой равномерной сходимостью на компактах (т. Е. Топологией, индуцированной компактно-открытой топологией на пространстве всех непрерывных функций из в ). ${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle T}$

Например,

${\ displaystyle {\ widehat {\ mathbb {Z}}} = T, \ {\ widehat {\ mathbb {R}}} = \ mathbb {R}, \ {\ widehat {T}} = \ mathbb {Z} .}$

Теорема двойственности Понтрягина

Теорема : существует канонический изоморфизм   между любой локально компактной абелевой группой и ее двойной двойственной.${\ Displaystyle G \ cong {\ widehat {\ widehat {G}}}}$${\ displaystyle G}$

Канонический означает, что существует естественно определенная карта  ; что еще более важно, карта должна быть функториальной в . Канонический изоморфизм определяется следующим образом: ${\ displaystyle \ operatorname {ev} _ {G} \ двоеточие G \ to {\ widehat {\ widehat {G}}}}$${\ displaystyle G}$${\ displaystyle \ operatorname {ev} _ {G}}$${\ displaystyle x \ in G}$

${\ displaystyle \ operatorname {ev} _ {G} (x) (\ chi) = \ chi (x) \ in \ mathbb {T}. \ {\ text {То есть}} \ \ operatorname {ev} _ {G} (x): (\ chi \ mapsto \ chi (x)).}$

Другими словами, каждый элемент группы идентифицируется с оценочным символом на дуале. Это сильно аналогично канонический изоморфизм между конечномерным векторным пространством и его двойным двойным , и стоит отметить , что любой вектор пространство является абелевой группой . Если - конечная абелева группа, то этот изоморфизм не канонический. Чтобы сделать это утверждение точным (в общем), необходимо подумать о дуализации не только на группах, но и на отображениях между группами, чтобы рассматривать дуализацию как функтор и доказать, что функтор тождества и функтор дуализации не являются естественно эквивалентными. Также из теоремы двойственности следует, что для любой группы (не обязательно конечной) функтор дуализации является точным функтором. ${\ displaystyle x}$${\ Displaystyle V \ cong V ^ {**}}$${\ displaystyle V}$${\ displaystyle G}$${\ Displaystyle G \ cong {\ widehat {G}}}$

Двойственность Понтрягина и преобразование Фурье

Мера Хаара

Один из самых замечательных фактов о локально компактной группе состоит в том, что она обладает существенно единственной естественной мерой , мерой Хаара , которая позволяет последовательно измерять «размер» достаточно регулярных подмножеств группы . «Достаточно регулярное подмножество» здесь означает борелевское множество ; то есть элемент σ-алгебры, порожденный компактами . Более точно, правая мера Хаара на локально компактной группе - это счетно-аддитивная мера μ, определенная на борелевских множествах, которая инвариантна справа в том смысле, что μ ( Ax ) = μ ( A ) для элемента и борелевского подмножества группы а также удовлетворяет некоторым условиям регулярности (подробно изложенным в статье о мере Хаара ). За исключением положительных масштабных коэффициентов, мера Хаара уникальна. ${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle x}$${\ displaystyle G}$${\ displaystyle A}$${\ displaystyle G}$${\ displaystyle G}$

Мера Хаара на позволяет нам определить понятие интеграла для борелевских ( комплекснозначных ) функций, определенных на группе. В частности, можно рассматривать различные L ^p- пространства, связанные с мерой Хаара µ. Конкретно, ${\ displaystyle G}$

${\ Displaystyle {\ mathcal {L}} _ {\ mu} ^ {p} (G) = \ left \ {(f: G \ to \ mathbb {C}) \ {\ Big |} \ \ int _ { G} | f (x) | ^ {p} \ d \ mu (x) <\ infty \ right \}.}$

Заметим, что, поскольку любые две меры Хаара на равны с точностью до масштабного коэффициента, это –пространство не зависит от выбора меры Хаара и, возможно, может быть записано как . Однако –норма в этом пространстве зависит от выбора меры Хаара, поэтому, если кто-то хочет говорить об изометриях, важно отслеживать используемую меру Хаара. ${\ displaystyle G}$${\ Displaystyle L ^ {p}}$${\ Displaystyle L ^ {p} (G)}$${\ Displaystyle L ^ {p}}$

Преобразование Фурье и формула обращения Фурье для L ¹ -функций

Двойственная группа локально компактной абелевой группы используется в качестве основного пространства для абстрактной версии преобразования Фурье . Если , то преобразование Фурье является функцией от определяются ${\ Displaystyle е \ в L ^ {1} (G)}$${\ displaystyle {\ widehat {f}}}$${\ displaystyle {\ widehat {G}}}$

${\ displaystyle {\ widehat {f}} (\ chi) = \ int _ {G} f (x) {\ overline {\ chi (x)}} \ d \ mu (x),}$

где интеграл относительно меры Хаара на . Это тоже обозначается . Обратите внимание, что преобразование Фурье зависит от выбора меры Хаара. Нетрудно показать, что преобразование Фурье функции на является ограниченной непрерывной функцией, которая обращается в нуль на бесконечности . ${\ displaystyle \ mu}$${\ displaystyle G}$${\ Displaystyle ({\ mathcal {F}} е) (\ чи)}$${\ displaystyle L ^ {1}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$

Формула обращения Фурье для -функций. ${\ displaystyle L ^ {1}}$Для каждой меры Хаара на существует единственная мера Хаара на такая, что всякий раз, когда и , мы имеем ${\ displaystyle \ mu}$${\ displaystyle G}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ Displaystyle е \ в L ^ {1} (G)}$${\ displaystyle {\ widehat {f}} \ in L ^ {1} \ left ({\ widehat {G}} \ right)}$

${\ Displaystyle е (х) = \ int _ {\ widehat {G}} {\ widehat {f}} (\ chi) \ chi (x) \ d \ nu (\ chi) \ qquad \ mu {\ text { -почти везде}}}$

Если непрерывно, то это тождество выполняется для всех .${\ displaystyle f}$${\ displaystyle x}$

Обратное преобразование Фурье интегрируемой функции на задаются ${\ displaystyle {\ widehat {G}}}$

${\ displaystyle {\ check {g}} (x) = \ int _ {\ widehat {G}} g (\ chi) \ chi (x) \ d \ nu (\ chi),}$

где интеграл относительно меры Хаара на дуальной группе . Мера на, которая появляется в формуле обращения Фурье, называется двойственной мерой к и может быть обозначена . ${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle \ mu}$${\ displaystyle {\ widehat {\ mu}}}$

Различные преобразования Фурье можно классифицировать с точки зрения их домена и области преобразования (группа и двойственная группа) следующим образом (обратите внимание, что это группа Circle ): ${\ Displaystyle \ mathbb {T}}$

Преобразовать	Исходный домен, ${\ displaystyle G}$	Преобразовать домен, ${\ displaystyle {\ hat {G}}}$	Мера, ${\ displaystyle \ mu}$
преобразование Фурье	${\ Displaystyle \ mathbb {R}}$	${\ Displaystyle \ mathbb {R}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {мера Лебега}}}$
Ряд Фурье	${\ Displaystyle \ mathbb {T}}$	${\ Displaystyle \ mathbb {Z}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {мера Лебега}}}$
Дискретное преобразование Фурье (ДВПФ)	${\ Displaystyle \ mathbb {Z}}$	${\ Displaystyle \ mathbb {T}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {счетная мера}}}$
Дискретное преобразование Фурье (ДПФ)	${\ Displaystyle \ mathbb {Z} _ {п}}$	${\ Displaystyle \ mathbb {Z} _ {п}}$	${\ displaystyle {\ text {Constant}} \ times {\ text {счетная мера}}}$

В качестве примера, предположу , так что мы можем думать о том, как спаривании Если есть мера Лебега на евклидово пространства, мы получаем обычное преобразование Фурье на и двойная мера необходимо для формулы обращения Фурье . Если мы хотим получить формулу обращения Фурье с одинаковой мерой с обеих сторон (то есть, поскольку мы можем рассматривать его как собственное двойственное пространство, которое мы можем попросить уравнять ), то нам нужно использовать ${\ Displaystyle G = \ mathbb {R} ^ {n}}$${\ displaystyle {\ widehat {G}}}$${\ Displaystyle \ mathbb {R} ^ {п}}$${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {i \ mathbf {v} \ cdot \ mathbf {w}}.}$${\ displaystyle \ mu}$${\ Displaystyle \ mathbb {R} ^ {п}}$${\ displaystyle {\ widehat {\ mu}} = (2 \ pi) ^ {- n} \ mu}$${\ Displaystyle \ mathbb {R} ^ {п}}$${\ displaystyle {\ widehat {\ mu}}}$${\ displaystyle \ mu}$

${\ displaystyle {\ begin {align} \ mu & = (2 \ pi) ^ {- {\ frac {n} {2}}} \ times {\ text {мера Лебега}} \\ {\ widehat {\ mu }} & = (2 \ pi) ^ {- {\ frac {n} {2}}} \ times {\ text {мера Лебега}} \ end {align}}}$

Однако, если мы изменим способ отождествления с его дуальной группой, используя пару ${\ Displaystyle \ mathbb {R} ^ {п}}$

${\ displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {2 \ pi i \ mathbf {v} \ cdot \ mathbf {w}},}$

то мера Лебега на равна своей собственной двойственной мере . Это соглашение сводит к минимуму количество факторов, которые появляются в различных местах при вычислении преобразований Фурье или обратных преобразований Фурье в евклидовом пространстве. (Фактически, это ограничивает только показателем степени, а не как предварительный фактор за пределами знака интеграла.) Обратите внимание, что выбор того, как идентифицировать свою двойственную группу, влияет на значение термина «самодвойственная функция», который является функция, равная своему собственному преобразованию Фурье: при использовании классического спаривания функция является самодвойственной. Но использование спаривания, которое сохраняет префактор как единство, вместо этого делает самодвойство. Это второе определение преобразования Фурье имеет то преимущество, что оно отображает мультипликативное тождество в тождество свертки, которое полезно, как алгебра свертки. См. Следующий раздел о групповой алгебре . Кроме того, эта форма также обязательно изометрична на пространствах. Ниже в Планшереле и L ² теоремы Фурьх инверсий${\ Displaystyle \ mathbb {R} ^ {п}}$${\ displaystyle 2 \ pi}$${\ displaystyle 2 \ pi}$${\ Displaystyle \ mathbb {R} ^ {п}}$${\ Displaystyle \ mathbb {R} ^ {п}}$${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto е ^ {я \ mathbf {v} \ cdot \ mathbf {w}}}$${\ displaystyle e ^ {- {\ frac {1} {2}} x ^ {2}}}$${\ Displaystyle (\ mathbf {v}, \ mathbf {w}) \ mapsto e ^ {2 \ pi {i} {\ mathbf {v}} \ cdot {\ mathbf {w}}}}$${\ displaystyle e ^ {- \ pi x ^ {2}}}$${\ displaystyle L ^ {1}}$${\ displaystyle L ^ {2}}$

Групповая алгебра

Пространство интегрируемых функций на локально компактной абелевой группе - это алгебра , где умножение - это свертка: свертка двух интегрируемых функций и определяется как ${\ displaystyle G}$${\ displaystyle f}$${\ displaystyle g}$

${\ Displaystyle (е * г) (х) = \ int _ {G} е (ху) г (у) \ д \ му (у).}$

Теорема. Банахово пространство является ассоциативной и коммутативной алгеброй относительно свертки.${\ Displaystyle L ^ {1} (G)}$

Эта алгебра называется групповой алгеброй с . По теореме Фубини-Тонелли , свертка полумультипликативная по отношению к норме, что делает в алгебру банахово . Банахова алгебра имеет мультипликативный единичный элемент тогда и только тогда, когда является дискретной группой, а именно функцией, которая равна единице в единице и нулю в другом месте. В общем, однако, он имеет приблизительную идентичность, которая представляет собой сеть (или обобщенную последовательность), проиндексированную на ориентированном множестве , так что${\ displaystyle G}$${\ displaystyle L ^ {1}}$${\ Displaystyle L ^ {1} (G)}$${\ Displaystyle L ^ {1} (G)}$${\ displaystyle G}$${\ Displaystyle \ {е_ {я} \} _ {я \ в I}}$${\ displaystyle I}$${\ displaystyle f * e_ {i} \ to f.}$

Преобразование Фурье переводит свертку в умножение, т.е. это гомоморфизм абелевых банаховых алгебр (нормы ≤ 1): ${\ Displaystyle L ^ {1} (G) \ к C_ {0} \ left ({\ widehat {G}} \ right)}$

${\ Displaystyle {\ mathcal {F}} (е * г) (\ чи) = {\ mathcal {F}} (е) (\ чи) \ cdot {\ mathcal {F}} (г) (\ чи) .}$

В частности, каждому групповому характеру на соответствует единственный мультипликативный линейный функционал на групповой алгебре, определяемый формулой ${\ displaystyle G}$

${\ displaystyle f \ mapsto {\ widehat {f}} (\ chi).}$

Важным свойством групповой алгебры является то, что они исчерпывают множество нетривиальных (т. Е. Не тождественно нулевых) мультипликативных линейных функционалов на групповой алгебре; см. раздел 34 ( Loomis 1953 ). Это означает, что преобразование Фурье является частным случаем преобразования Гельфанда .

Планшерелевой и L ² теоремы Фурье инверсии

Как мы заявляли, двойственная группа локально компактной абелевой группы является локально компактной абелевой группой сама по себе и, следовательно, имеет меру Хаара, или, точнее, целое семейство мер Хаара, связанных с масштабом.

Теорема. Выберите меру Хаара на и пусть будет двойная мера на, как определено выше. Если непрерывна с компактной опорой, то и ${\ displaystyle \ mu}$${\ displaystyle G}$${\ displaystyle \ nu}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle f: G \ to \ mathbb {C}}$${\ displaystyle {\ widehat {f}} \ in L ^ {2} \ left ({\ widehat {G}} \ right)}$

${\ Displaystyle \ int _ {G} | е (х) | ^ {2} \ d \ mu (x) = \ int _ {\ widehat {G}} \ left | {\ widehat {f}} (\ chi ) \ right | ^ {2} \ d \ nu (\ chi).}$

В частности, преобразование Фурье является изометрией из комплекснозначных непрерывных функций с компактным носителем на к -функции на ( с использованием -норма по отношению к ц для функций на и -норм относительно v , для функций на ).${\ displaystyle L ^ {2}}$${\ displaystyle G}$${\ displaystyle L ^ {2}}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle L ^ {2}}$${\ displaystyle G}$${\ displaystyle L ^ {2}}$${\ displaystyle {\ widehat {G}}}$

Поскольку комплекснозначные непрерывные финитных функции на это -плотное, существует единственное продолжение преобразования Фурье из этого пространства к унитарному оператору${\ displaystyle G}$${\ displaystyle L ^ {2}}$

${\ displaystyle {\ mathcal {F}}: L _ {\ mu} ^ {2} (G) \ to L _ {\ nu} ^ {2} \ left ({\ widehat {G}} \ right).}$

и у нас есть формула

${\ displaystyle \ forall f \ in L ^ {2} (G): \ quad \ int _ {G} | f (x) | ^ {2} \ d \ mu (x) = \ int _ {\ widehat { G}} \ left | {\ widehat {f}} (\ chi) \ right | ^ {2} \ d \ nu (\ chi).}$

Обратите внимание, что для некомпактных локально компактных групп пространство не содержит , поэтому преобразование Фурье общих -функций на «не» задается какой-либо формулой интегрирования (или действительно любой явной формулой). Чтобы определить преобразование Фурье, нужно прибегнуть к некоторой технической уловке, например, начать с плотного подпространства, такого как непрерывные функции с компактным носителем, а затем продолжить изометрию по непрерывности на все пространство. Это унитарное расширение преобразования Фурье и есть то, что мы понимаем под преобразованием Фурье на пространстве функций, интегрируемых с квадратом. ${\ displaystyle G}$${\ Displaystyle L ^ {1} (G)}$${\ Displaystyle L ^ {2} (G)}$${\ displaystyle L ^ {2}}$${\ displaystyle G}$${\ displaystyle L ^ {2}}$

Двойственная группа также имеет собственное обратное преобразование Фурье; его можно охарактеризовать как обратное (или сопряженное, поскольку оно унитарно) преобразования Фурье. Это содержание следующей формулы обращения Фурье. ${\ displaystyle L ^ {2}}$${\ displaystyle L ^ {2}}$

Теорема. Сопряжением преобразования Фурье, ограниченного непрерывными функциями компактного носителя, является обратное преобразование Фурье

${\ Displaystyle L _ {\ nu} ^ {2} \ left ({\ widehat {G}} \ right) \ к L _ {\ mu} ^ {2} (G)}$

где двойственная мера к .${\ displaystyle \ nu}$${\ displaystyle \ mu}$

В случае, когда двойственная группа естественно изоморфна группе целых чисел, а преобразование Фурье специализируется на вычислении коэффициентов рядов Фурье периодических функций. ${\ Displaystyle G = \ mathbb {T}}$${\ displaystyle {\ widehat {G}}}$${\ Displaystyle \ mathbb {Z}}$

Если - конечная группа, мы восстанавливаем дискретное преобразование Фурье . Отметим, что этот случай очень легко доказать напрямую. ${\ displaystyle G}$

Компактификация Бора и почти периодичность

Одним из важных приложений двойственности Понтрягина является следующая характеризация компактных абелевых топологических групп:

Теорема . Локально компактная абелева группа компактна тогда и только тогда, когда двойственная группа дискретна. Наоборот, дискретно тогда и только тогда, когда компактно.${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$

Это будучи компактным подразумеваешь дискретно или что является дискретным означает , что компактно является элементарным следствием определения компактно-открытой топологии и не нуждается в Понтрягине. Для доказательства обратного используется двойственность Понтрягина. ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ widehat {G}}}$

Компактификация Бора определяется для любой топологической группы , независимо от того , является локально компактной или абелева. Одно из применений двойственности Понтрягина между компактными абелевыми группами и дискретными абелевыми группами состоит в том, чтобы охарактеризовать боровскую компактификацию произвольной абелевой локально компактной топологической группы. Бор компактификацией из является , где Н имеет групповую структуру , но с учетом дискретной топологией . Поскольку карта включения${\ displaystyle G}$${\ displaystyle G}$ ${\ Displaystyle B (G)}$${\ displaystyle G}$${\ displaystyle {\ widehat {H}}}$${\ displaystyle {\ widehat {G}}}$

${\ displaystyle \ iota: H \ to {\ widehat {G}}}$

является непрерывным и гомоморфизмом, двойственный морфизм

${\ displaystyle G \ sim {\ widehat {\ widehat {G}}} \ to {\ widehat {H}}}$

является морфизмом в компактную группу, которая, как легко показать, удовлетворяет требуемому универсальному свойству .

См. Также почти периодическую функцию .

Категориальные соображения

Двойственность Понтрягина также может быть выгодно рассмотрена функториально . В дальнейшем LCA - это категория локально компактных абелевых групп и непрерывных гомоморфизмов групп. Двойная группа конструкция представляет собой контравариантный функтор ДМС → LCA , представлен (в том смысле , представимых функторы ) группа окружности , как , в частности, двойной двойственный функтор является ковариантным . Затем категоричная формулировка двойственности Понтрягина утверждает, что естественное преобразование между тождественным функтором на LCA и двойным двойственным функтором является изоморфизмом. Разворачивая понятие естественного преобразования, это означает, что отображения являются изоморфизмами для любой локально компактной абелевой группы , и эти изоморфизмы функториальны в . Этот изоморфизм является аналогом двойной двойной из конечномерных векторных пространств (частный случай, для вещественных и комплексных векторных пространств). ${\ displaystyle {\ widehat {G}}}$${\ Displaystyle \ mathbb {T}}$${\ displaystyle {\ widehat {G}} = {\ text {Hom}} (G, \ mathbb {T}).}$${\ displaystyle G \ to {\ widehat {\ widehat {G}}}}$${\ displaystyle G \ to \ operatorname {Hom} (\ operatorname {Hom} (G, T), T)}$${\ displaystyle G}$${\ displaystyle G}$

Непосредственным следствием этой формулировки является другая распространенная категориальная формулировка двойственности Понтрягина: двойственный групповой функтор является эквивалентностью категорий от LCA до LCA ^op .

Двойственность меняет местами подкатегории дискретных групп и компактных групп . Если это кольцо и является левым - модуль , двойная группа станет правым модулем; таким образом мы также видим, что дискретные левые –модули будут двойственными по Понтрягину компактным правым –модулям. Кольцо из эндоморфизмов в LCA изменяется по двойственности в его противоположное кольцо (изменить умножение на другой порядок). Например, если - бесконечная циклическая дискретная группа, - это круговая группа: первая имеет, поэтому это верно также и для второй. ${\ displaystyle R}$${\ displaystyle G}$${\ displaystyle R}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle {\ text {End}} (G)}$${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle {\ text {End}} (G) = \ mathbb {Z}}$

Обобщения

Обобщения двойственности Понтрягина строятся в двух основных направлениях: для коммутативных топологических групп , не являющихся локально компактными , и для некоммутативных топологических групп. Теории в этих двух случаях очень разные.

Двойственности коммутативных топологических групп

Когда является хаусдорфовой абелевой топологической группой, группа с компактно-открытой топологией является хаусдорфовой абелевой топологической группой и имеет смысл естественное отображение из в ее дважды-двойственную группу . Если это отображение является изоморфизмом, говорят, что оно удовлетворяет двойственности Понтрягина (или это рефлексивная группа , или рефлексивная группа ). Это было расширено в ряде направлений за пределы локально компактного случая . ${\ displaystyle G}$${\ displaystyle {\ widehat {G}}}$${\ displaystyle G}$${\ displaystyle {\ widehat {\ widehat {G}}}}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$

В частности, Самуэль Каплан показал в 1948 и 1950 годах, что произвольные произведения и счетные обратные пределы локально компактных (хаусдорфовых) абелевых групп удовлетворяют двойственности Понтрягина. Отметим, что бесконечное произведение локально компактных некомпактных пространств не является локально компактным.

Позже, в 1975 году, Рангачари Венкатараман показал, среди прочего, что каждая открытая подгруппа абелевой топологической группы, удовлетворяющая двойственности Понтрягина, сама удовлетворяет двойственности Понтрягина.

Совсем недавно Серджио Арданса-Тревихано и Мария Хесус Часко расширили результаты Каплана, упомянутые выше. Они показали, что прямые и обратные пределы последовательностей абелевых групп, удовлетворяющих двойственности Понтрягина, также удовлетворяют двойственности Понтрягина, если группы являются метризуемыми или -пространствами, но не обязательно локально компактными, при условии, что последовательности удовлетворяют некоторым дополнительным условиям. ${\ displaystyle k _ {\ omega}}$

Однако есть фундаментальный аспект, который меняется, если мы хотим рассматривать двойственность Понтрягина вне локально компактного случая. Елена Мартин-Пейнадор доказала в 1995 году, что если - хаусдорфова абелева топологическая группа, удовлетворяющая двойственности Понтрягина, и естественная пара вычислений ${\ displaystyle G}$

${\ displaystyle {\ begin {cases} G \ times {\ widehat {G}} \ to \ mathbb {T} \\ (x, \ chi) \ mapsto \ chi (x) \ end {cases}}}$

непрерывно (совместно), то локально компактно. Как следствие, все нелокально компактные примеры двойственности Понтрягина - это группы, в которых спаривание не (совместно) непрерывно. ${\ displaystyle G}$${\ Displaystyle G \ times {\ widehat {G}} \ to \ mathbb {T}}$

Другой способ обобщить двойственность Понтрягина на более широкие классы коммутативных топологических групп - снабдить двойственную группу немного другой топологией, а именно топологией равномерной сходимости на вполне ограниченных множествах . Группы, удовлетворяющие тождеству при этом предположении, называются стереотипными группами . Этот класс также очень широк (и содержит локально компактные абелевы группы), но уже, чем класс рефлексивных групп. ${\ displaystyle {\ widehat {G}}}$${\ Displaystyle G \ cong {\ widehat {\ widehat {G}}}}$

Двойственность Понтрягина для топологических векторных пространств

В 1952 году Марианна Ф. Смит заметила, что банаховы пространства и рефлексивные пространства , рассматриваемые как топологические группы (с операцией аддитивной группы), удовлетворяют двойственности Понтрягина. Позднее Б. С. Брудовский, Уильям К. Уотерхаус и К. Браунер показали, что этот результат может быть распространен на класс всех квазиполных бочкообразных пространств (в частности, на все пространства Фреше ). В 1990-е годы Сергей Акбаров дал описание класса топологических векторных пространств, которые удовлетворяют более сильному свойству, чем классическая рефлексивность Понтрягина, а именно тождеству

${\ Displaystyle (Х ^ {\ звезда}) ^ {\ звезда} \ cong X}$

где означает пространство всех линейных непрерывных функционалов, наделенных топологией равномерной сходимости на вполне ограниченных множествах в (и означает двойственное к в том же смысле). Пространства этого класса называются стереотипными пространствами , и соответствующая теория нашла ряд приложений в функциональном анализе и геометрии, включая обобщение двойственности Понтрягина для некоммутативных топологических групп. ${\ Displaystyle X ^ {\ звезда}}$${\ displaystyle f \ двоеточие X \ to {\ mathbb {C}}}$${\ displaystyle X}$${\ Displaystyle (Х ^ {\ звезда}) ^ {\ звезда}}$${\ Displaystyle X ^ {\ звезда}}$

Двойственности для некоммутативных топологических групп

Для некоммутативных локально компактных групп классическая конструкция Понтрягина перестает работать по разным причинам, в частности из-за того, что характеры не всегда разделяют точки группы , а неприводимые представления группы не всегда одномерны. В то же время неясно, как ввести умножение на множестве неприводимых унитарных представлений , и даже неясно, подходит ли это множество для роли двойственного объекта для . Так что проблема построения двойственности в этой ситуации требует полного переосмысления. ${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$

Теории, построенные на сегодняшний день, делятся на две основные группы: теории, в которых дуальный объект имеет ту же природу, что и исходный (как в самой дуальности Понтрягина), и теории, в которых исходный объект и его двойник столь радикально отличаются друг от друга. что их нельзя считать объектами одного класса.

Теории второго типа исторически были первыми: вскоре после работы Понтрягина Тадао Таннака (1938) и Марк Крейн (1949) построили теорию двойственности для произвольных компактных групп, известную теперь как двойственность Таннаки – Крейна . В этой теории двойственным объектом для группы является не группа, а категория ее представлений . ${\ displaystyle G}$ ${\ Displaystyle \ Pi (G)}$

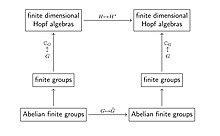
Теории первого типа появились позже, и ключевым примером для них была теория двойственности для конечных групп. В этой теории категория конечных групп вкладывается операцией перевода групповой алгебры (над ) в категорию конечномерных алгебр Хопфа , так что функтор двойственности Понтрягина превращается в операцию взятия двойственного векторного пространства (что является двойственностью функтор в категории конечномерных алгебр Хопфа). ${\ Displaystyle G \ mapsto {\ mathbb {C}} _ ​​{G}}$ ${\ Displaystyle {\ mathbb {C}} _ ​​{G}}$${\ Displaystyle {\ mathbb {C}}}$${\ Displaystyle G \ mapsto {\ widehat {G}}}$${\ Displaystyle H \ mapsto H ^ {*}}$

В 1973 г. Леонид И. Вайнерман, Георгий И. Кац, Мишель Энок и Жан-Мари Шварц построили общую теорию этого типа для всех локально компактных групп. С 1980-х годов исследования в этой области были возобновлены после открытия квантовых групп , на которые начали активно переноситься построенные теории. Эти теории сформулированы на языке C * -алгебр или алгебр фон Неймана , и одним из ее вариантов является недавняя теория локально компактных квантовых групп .

Однако одним из недостатков этих общих теорий является то, что в них объекты, обобщающие понятие группы, не являются алгебрами Хопфа в обычном алгебраическом смысле. Этот недостаток можно исправить (для некоторых классов групп) в рамках теорий двойственности, построенных на основе понятия оболочки топологической алгебры.

Смотрите также

• Теорема Питера – Вейля
• Картье двойственность
• Пространство стереотипов

Примечания

использованная литература

• Диксмье, Жак (1969). Les C * -algèbres et leurs Représentations . Готье-Виллар. ISBN 978-2-87647-013-2.
• Энок, Мишель; Шварц, Жан-Мари (1992). Алгебры Каца и двойственность локально компактных групп . С предисловием Алена Конна. С постфайсом Адриана Окнеану. Берлин: Springer-Verlag. DOI : 10.1007 / 978-3-662-02813-1 . ISBN 978-3-540-54745-7. Руководство по ремонту  1215933 .
• Хьюитт, Эдвин; Росс, Кеннет А. (1963). Абстрактный гармонический анализ. Vol. I: Структура топологических групп. Теория интеграции, представления групп . Die Grundlehren der Mathematischen Wissenschaften. 115 . Берлин-Геттинген-Гейдельберг: Springer-Verlag. ISBN 978-0-387-94190-5. Руководство по ремонту  0156915 .
• Хьюитт, Эдвин; Росс, Кеннет А. (1970). Абстрактный гармонический анализ . 2 . ISBN 978-3-662-24595-8. Руководство по ремонту  0262773 .
• Кириллов, Александр А. (1976) [1972]. Элементы теории представлений . Grundlehren der Mathematischen Wissenschaften. 220 . Берлин, Нью-Йорк: Springer-Verlag . ISBN 978-0-387-07476-4. Руководство по ремонту  0412321 .
• Лумис, Линн Х. (1953). Введение в абстрактный гармонический анализ . D. van Nostrand Co. ISBN 978-0486481234.
• Моррис, С.А. (1977). Двойственность Понтрягина и строение локально компактных абелевых групп . Издательство Кембриджского университета . ISBN 978-0521215435.
• Онищик А.Л. (1984). Понтрягина двойственность . Энциклопедия математики . 4 . С. 481–482. ISBN 978-1402006098.
• Райтер, Ганс (1968). Классический гармонический анализ и локально компактные группы . ISBN 978-0198511892.
• Рудин, Вальтер (1962). Фурье-анализ на группах . D. van Nostrand Co. ISBN 978-0471523642.
• Тиммерманн, Т. (2008). Приглашение к квантовым группам и двойственности - от алгебр Хопфа к мультипликативным унитарным и не только . Учебники EMS по математике, Европейское математическое общество. ISBN 978-3-03719-043-2.
• Kustermans, J .; Ваес, С. (2000). «Локально компактные квантовые группы» . Annales Scientifiques de l'École Normale Supérieure . 33 (6): 837–934. DOI : 10.1016 / s0012-9593 (00) 01055-7 .
• Арданца-Тревихано, Серхио; Часко, Мария Хесус (2005). «Двойственность Понтрягина секвенциальных пределов топологических абелевых групп». Журнал чистой и прикладной алгебры . 202 (1–3): 11–21. DOI : 10.1016 / j.jpaa.2005.02.006 . hdl : 10171/1586 . Руководство по ремонту  2163398 .
• Часко, Мария Хесус; Дикранджан, Дикран; Мартин-Пейнадор, Елена (2012). «Обзор рефлексивности абелевых топологических групп» . Топология и ее приложения . 159 (9): 2290–2309. DOI : 10.1016 / j.topol.2012.04.012 . Руководство по ремонту  2921819 .
• Каплан, Самуэль (1948). «Расширения двойственности Понтрягина. Часть I: бесконечные произведения». Математический журнал герцога . 15 : 649–658. DOI : 10.1215 / S0012-7094-48-01557-9 . Руководство по ремонту  0026999 .
• Каплан, Самуэль (1950). «Расширения двойственности Понтрягина. Часть II: прямые и обратные пределы». Математический журнал герцога . 17 : 419–435. DOI : 10.1215 / S0012-7094-50-01737-6 . Руководство по ремонту  0049906 .
• Венкатараман, Рангачари (1975). «Расширения двойственности Понтрягина». Mathematische Zeitschrift . 143 (2): 105–112. DOI : 10.1007 / BF01187051 . S2CID  123627326 .
• Мартин-Пейнадор, Елена (1995). «Рефгибкая допустимая топологическая группа должна быть локально компактной». Труды Американского математического общества . 123 (11): 3563–3566. DOI : 10.2307 / 2161108 . hdl : 10338.dmlcz / 127641 . JSTOR  2161108 .
• Смит, Марианна Ф. (1952). «Теорема двойственности Понтрягина в линейных пространствах». Анналы математики . 56 (2): 248–253. DOI : 10.2307 / 1969798 . JSTOR  1969798 . Руководство по ремонту  0049479 .
• Брудовский, Б.С. (1967). «О k- и c-рефлексивности локально выпуклых векторных пространств». Литовский математический журнал . 7 (1): 17–21.
• Уотерхаус, Уильям К. (1968). «Двойственные группы векторных пространств» . Тихоокеанский математический журнал . 26 (1): 193–196. DOI : 10,2140 / pjm.1968.26.193 .
• Браунер, Кальман (1973). «Двойники пространств Фреше и обобщение теоремы Банаха – Дьедонне». Математический журнал герцога . 40 (4): 845–855. DOI : 10.1215 / S0012-7094-73-04078-7 .
• Акбаров, С.С. (2003). «Двойственность Понтрягина в теории топологических векторных пространств и в топологической алгебре». Журнал математических наук . 113 (2): 179–349. DOI : 10,1023 / А: 1020929201133 . S2CID  115297067 .
• Акбаров, Сергей С .; Шавгулидзе, Евгений Т. (2003). «О двух классах пространств, рефлексивных по Понтрягина» . Математический сборник . 194 (10): 3–26.
• Акбаров, Сергей С. (2009). «Голоморфные функции экспоненциального типа и двойственности для групп Штейна с алгебраической связной компонентой единицы». Журнал математических наук . 162 (4): 459–586. arXiv : 0806.3205 . DOI : 10.1007 / s10958-009-9646-1 . S2CID  115153766 .
• Акбаров, Сергей С. (2017). «Непрерывные и гладкие оболочки топологических алгебр. Часть 1». Журнал математических наук . 227 (5): 531–668. arXiv : 1303,2424 . DOI : 10.1007 / s10958-017-3599-6 . Руководство по ремонту  3790317 . S2CID  126018582 .
• Акбаров, Сергей С. (2017). «Непрерывные и гладкие оболочки топологических алгебр. Часть 2». Журнал математических наук . 227 (6): 669–789. arXiv : 1303,2424 . DOI : 10.1007 / s10958-017-3600-4 . Руководство по ремонту  3796205 . S2CID  128246373 .